Основні залежності механіки стержнів. Рівняння статичної, геометричної і фізичної сторін задачі для стержня
1. Статична сторона задачі. Рівняння рівноваги
Розглянемо нескінченно малий елемент стержня.
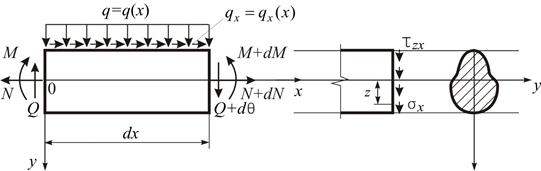
Рис. 3.1
Інтегральні характеристики
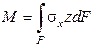 ,
, 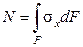 ,
, 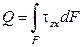 .
.
Приріст кожного із зусиль визначається так:
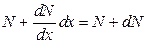 .
.
Отримаємо рівняння рівноваги у вигляді :
1. 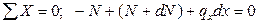
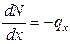
2. 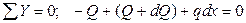
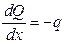
3. 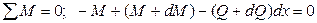
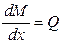
2. Геометрична сторона задачі. Зв'язок між деформаціями і переміщеннями
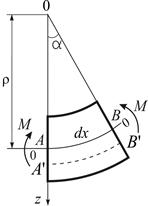 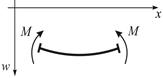 Рис. 3.2
Рис. 3.2
| Деформація 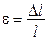
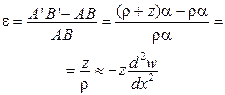
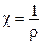 - кривизна - кривизна
|

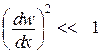 береться «мінус»
береться «мінус»
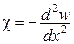 .
.
Приклад
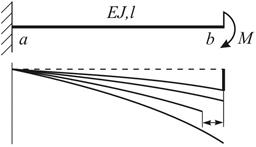 Рис. 3.3
Рис. 3.3
| Насправді, при так званих “великих переміщеннях (див. рис. 3.3) мають місце не тільки вертикальні, а і горизонтальні переміщення точок стержня. Але в елементарній лінійній теорії згину вважається, що  і цей ефект не враховується. і цей ефект не враховується.
|
3. Фізична сторона задачі. Закон Гука
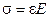 ,
, 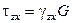 ,
,
де G – модуль зсуву, Е – модуль пружності (модуль Юнга).
 (наприклад, для металу Е=2 105 Мпа),
(наприклад, для металу Е=2 105 Мпа),
де µ- коефіцієнт Пуассона (залежність між поперечними і повздовжніми деформаціями), µ=0…0,5.
Найпростіший напружений стан – розтяг-стиснення (див. рис. 3.4)
 Рис. 3.4
Рис. 3.4
| 1) 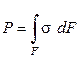 2)
2) 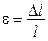 3)
3) 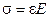 закон Гука* закон Гука*
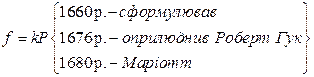
|
Розрахував коефіцієнт k Томас Юнг в 1807 р.
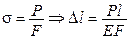 .
.
Кулон у 1784 році отримав при скрученні стержня залежність
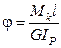 .
.
А.Навьє в 1826 році ввів поняття напруження і отримав
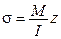 ,
,
тобто через 150 років після оприлюднення закону Гука.
Далі Коші ввів поняття про головні напруження
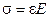 ,
,
а Пуассон ввів коефіцієнт 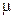 .
.
Тобто, до фундаментальних понять про напруження і деформації людство йшло майже два століття, хоч впритул до цього наблизився Юнг і навіть близько був ще Галілей.
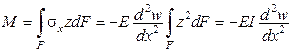 ,
,
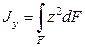 ,
,
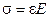 .
.
 |
* Цікавою є історія становлення закону Гука. Знаний англійський учений Роберт Гук в 1660 р. сформулював, а в 1676 р. оприлюднив, і то у вигляді анаграми, таке: «яка деформація, таке і навантаження» (навіть не навпаки). Майже одночсасно з Гуком (1680 р.) і незалежно від нього цей закон сформулював француз Маріотт: «навіть найбільш тверді тіла – скло і залізо – деформуються пропорційно навантаженню». Тобто,  , де P – навантаження, f – деформація стержня, k – коефіцієнт пропорційності. Розшифрування коефіцієнта k стало можливим через 130 років, коли англієць Томас Юнг у 1807 р. ввів поняття про модуль пружності Е, названий його ім’ям. Тепер можна було записати
, де P – навантаження, f – деформація стержня, k – коефіцієнт пропорційності. Розшифрування коефіцієнта k стало можливим через 130 років, коли англієць Томас Юнг у 1807 р. ввів поняття про модуль пружності Е, названий його ім’ям. Тепер можна було записати  , де l – довжина стержня, F – площа поперечного перерізу, Е – модуль Юнга, Р – навантаження (сила). Юнг же і визначив значення Е для сталей, як 2·105 МПа. У 1784 р. французький фізик Кулон сформулював закон Гука при скрученні стержня
, де l – довжина стержня, F – площа поперечного перерізу, Е – модуль Юнга, Р – навантаження (сила). Юнг же і визначив значення Е для сталей, як 2·105 МПа. У 1784 р. французький фізик Кулон сформулював закон Гука при скрученні стержня 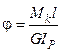 . У 1826 р. французький інженер (потім академік) А.Нав’є видав перший підручник з опору матеріалів, в якому ввів поняття про напруження (як силу, що діє на одиницю площі перерізу) і записав
. У 1826 р. французький інженер (потім академік) А.Нав’є видав перший підручник з опору матеріалів, в якому ввів поняття про напруження (як силу, що діє на одиницю площі перерізу) і записав 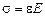 (через 150 років після оприлюднення закону Гука), а також отримав відому формулу для нормальних напружень при згині стержня
(через 150 років після оприлюднення закону Гука), а також отримав відому формулу для нормальних напружень при згині стержня 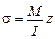 . Згодом Нав’є ввів поняття про допустимі напруження, умову міцності, О.Коші – поняття про головні напруження і головні деформації, Пуассон ввів свій «коефіцієнт Пуассона». Таким чином, загальними зусиллями в основному цих трьох видатних французів закон Гука постав у закінченому вигляді «узагальненого закону Гука». Тобто, до фундаментальних понять про напруження і деформації людство йшло майже два століття, хоч до них впритул наблизився Юнг і, навіть, близько був ще Галілей (1564-1642).
. Згодом Нав’є ввів поняття про допустимі напруження, умову міцності, О.Коші – поняття про головні напруження і головні деформації, Пуассон ввів свій «коефіцієнт Пуассона». Таким чином, загальними зусиллями в основному цих трьох видатних французів закон Гука постав у закінченому вигляді «узагальненого закону Гука». Тобто, до фундаментальних понять про напруження і деформації людство йшло майже два століття, хоч до них впритул наблизився Юнг і, навіть, близько був ще Галілей (1564-1642).
Деформація  .
.
Постановка крайової задачі механіки стержнів у зусиллях і переміщеннях.
Розглянемо балку.
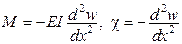 - рівняння сумісності деформацій, - рівняння сумісності деформацій, 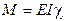 . .
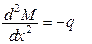 - рівняння рівноваги. - рівняння рівноваги.
| (*) |
Граничні умови
 Рис. 3.5
Рис. 3.5
| 
 Будемо умовно вважати, що індексами «1» позначені точки, у яких задані силові характеристики
Будемо умовно вважати, що індексами «1» позначені точки, у яких задані силові характеристики
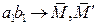 , ,
|
а індексами «2», відповідно, точки, у я ких задані кінематичні характеристики
 .
.
Рівняння (*) можна звести до одного рівняння і отримати постановку крайової задачі механіки стержнів у переміщеннях
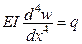 .
.
При цьому
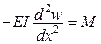 ,
, 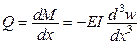 .
.
Тоді граничні умови
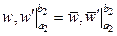 ,
,  ,
, 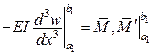 .
.
Лекція 4
Дата добавления: 2016-12-26; просмотров: 943;
