Варіаційні рівняння для функціоналів Лагранжа і Кастільяно

Розглянемо першу варіацію функціонала Кастільяно, який запишемо з урахуванням залежності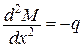

.

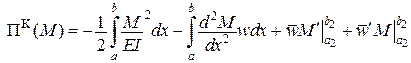Будемо вважати для спрощення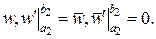

Тоді

.

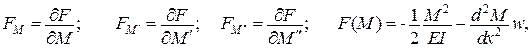
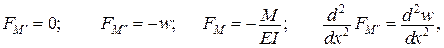
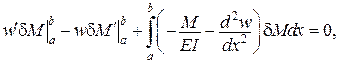
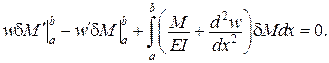Варіаційне рівняння для функціонала Кастільяно

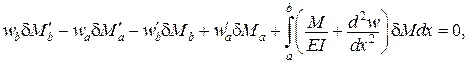
у випадку коли

.

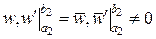У загальному випадку

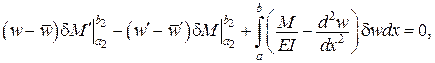
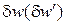- змінюються переміщення - (принцип Лагранжа),

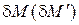- змінюються зусилля - (принцип Кастільяно).

Зазначимо, що наведені варіаційні рівняння Лагранжа і Кастільяно можуть бути отримані і безпосередньо із залежностей (____) підстановкою відповідно 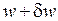і .

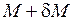Наприклад, підставляючи 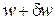, отримаємо вираз, який залежить від першої варіації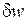

.

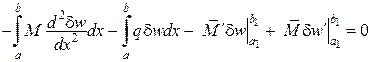Перший інтеграл за формулою Гріна дорівнює

.

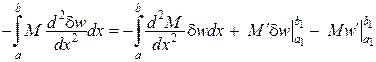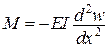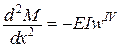Ураховуючи, що і , остаточно одержимо

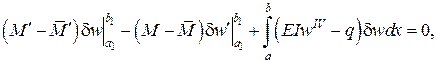
що являє собою _____.

Аналогічно, підставляючи 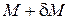, отримаємо вираз, який залежить від першої варіації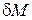

.

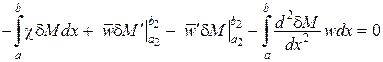Перший інтеграл

.

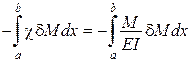Другий інтеграл за формулою Гріна дорівнює

.

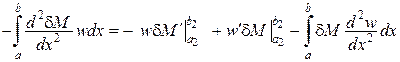і остаточно одержимо

,

,

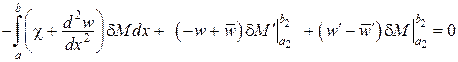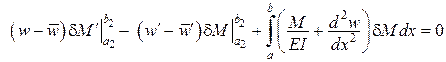що являє собою розгорнутий вигляд варіаційного рівняння Кастільяно .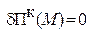

Розглянемо варіаційні рівняння Лагранжа і Кастільяно при однорідних граничних умовах

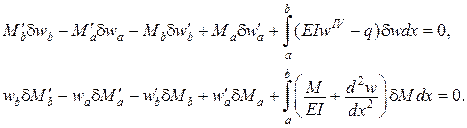
Для різних граничних умов отримаємо (див. табл.)

Таблиця

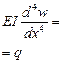
Задані зовні гран. умови w, w’	wa=0 wb=0   w’a=0 w’b=0	wa=0 wb=0   w’a=0 -----	wa=0 -----   w’a=0 -----	wa=0 wb=0   ----- -----	Природ. граничні умови	Лаграрж
Природ. граничні умови	----- ----- ----- -----	----- ----- ----- Mb=0	----- M’b=0 ----- Mb=0	----- ----- Ma=0 Mb=0	Задані зовні гран. умови w, w’	Кастільяно

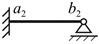
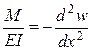
Таким чином, реалізація принципу Лагранжа дозволяє автоматично отримати рівняння рівноваги, як рівняння Ейлера відповідної варіаційної задачі 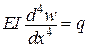, а також граничні умови, яких не вистачало, у вигляді так званих природних граничних умов. У таблиці це показано для балок з різними однорідними граничними умовами 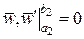.	Таким чином, реалізація принципу Кастільяно дозволяє автоматично отримати рівняння сумісності деформацій, як рівняння Ейлера відповідної варіаційної задачі 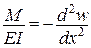, а також граничні умови, яких не вистачало, у вигляді так званих природних граничних умов (див. таблицю, при ).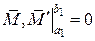
Варіаційне рівняння Лагранжа 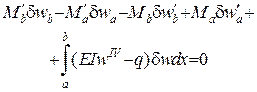являє собою широко відомий принцип можливих переміщень, а саме: якщо сума робіт усіх зусиль на будь-яких можливих. переміщеннях дорівнює 0, то система знаходиться в рівновазі.	Варіаційне рівняння Кастільяно 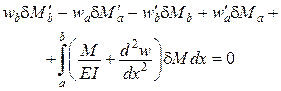являє собою широко відомий принцип можливих зусиль, а саме: якщо сума робіт усіх зусиль при будь-яких змінах напруженого стану дорівнює 0, то виконуються умови сумісності деформацій.

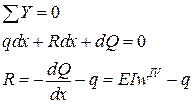
Лекція 7