Приклади реалізації принципів Лагранжа і Кастільяно.
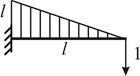
Розглянемо розв'язання задачі згину балки (рис. 8.6), яка має кінематичне навантаження у вигляді просідання правої опори на величину 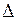 , користуючись принципами
, користуючись принципами
| Лагранжа | Принцип Кастільяно |
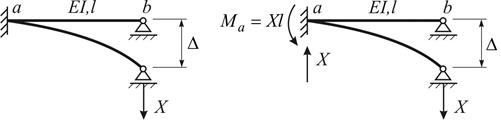 Рис. 8.6
Рис. 8.6
| |
Функціонал Лагранжа для даної задачі має вигляд:
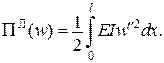
| Функціонал Кастільяно для даної задачі має вигляд:
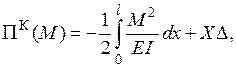
|
Додаткові умови
 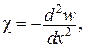
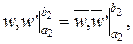
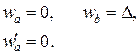
| Додаткові умови
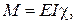 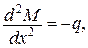 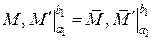 ,
або ,
або
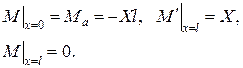
|
Задаємо функцію прогину 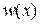 у вигляді ряду: у вигляді ряду:
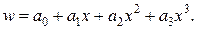 Тоді
Тоді
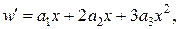
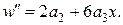
| Задаємо функцію 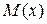 у вигляді ряду: у вигляді ряду:
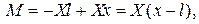 який задовольняє статичним граничним умовам і умові рівноваги
який задовольняє статичним граничним умовам і умові рівноваги
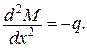
|
Реалізація граничних умов дає:
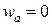 , , 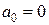 , ,
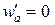 , , 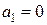 , ,
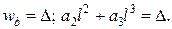 ,
Звідси ,
Звідси
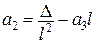 і
і
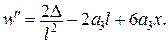
| |
Тоді
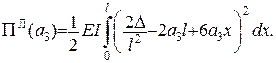
| Тоді
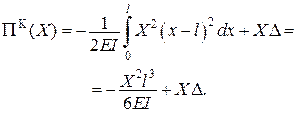
|
Принцип Лагранжа
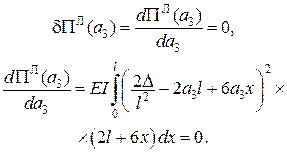
| Принцип Кастільяно
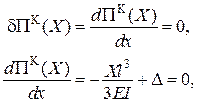
|
Інтегруючи і розв’язуючи відповідне рівняння, отримаємо
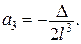 Тоді
Тоді
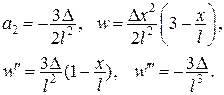
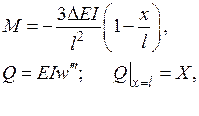
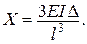
| 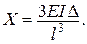 Ураховуючи, що
Ураховуючи, що
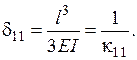 Рівняння методу сил має вигляд
Рівняння методу сил має вигляд
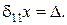
|
Екстремальне значення функціо-нала Лагранжа дорівнює
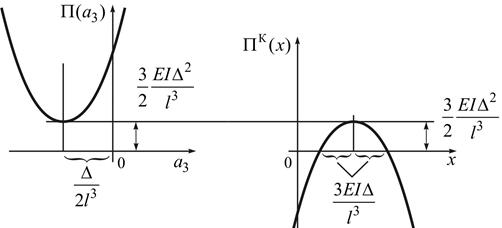
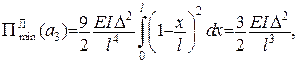 а залежність а залежність 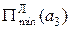 від від 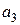 показана на рис. 8.7, а. показана на рис. 8.7, а.
| Екстремальне значення функціо-нала Кастільяно дорівнює
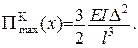 Оскільки
Оскільки
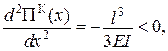 Це є максимум, а залежність
Це є максимум, а залежність 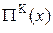 від x показана на рис. 8.7, б. від x показана на рис. 8.7, б.
|
| |
| а | б |
| Рис. 8.7 |
Таким чином екстремальні значення функціоналів Лагранжа і Кастільяно співпадають.
Функціонал Лагранжа інколи називається повною потенціальною енергією системи і дорівнює сумі потенціальної енергій пружної деформації і роботи зовнішніх сил.

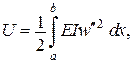
 .
.
 При цьому потенціальна енергія пружної деформації ототожнюється з роботою внутрішніх сил і є позитивною. Робота зовнішніх сил обчислюється як добуток сили на відповідне переміщення (без коефіцієнту ½) і вважається негативною. Функціонал Лагранжа або повна потенціальна енергія інколи трактується як енергія, яка витрачається при переході системи від деформованого стану до первісного.
При цьому потенціальна енергія пружної деформації ототожнюється з роботою внутрішніх сил і є позитивною. Робота зовнішніх сил обчислюється як добуток сили на відповідне переміщення (без коефіцієнту ½) і вважається негативною. Функціонал Лагранжа або повна потенціальна енергія інколи трактується як енергія, яка витрачається при переході системи від деформованого стану до первісного.
Дата добавления: 2016-12-26; просмотров: 774;
