Канонічні рівняння методу Бубнова-Гальоркіна для функціонала Лагранжа. Приклад

Наведемо розв’язок за методом Рітца іншої задачі (рис. 11.1). Природньо, що порівняно із попередньою (рис. 11.2) тут змінюється вектор навантажень:

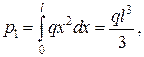
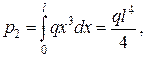
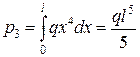
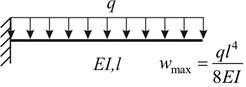Рис. 11.1 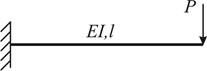Рис. 11.2

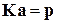, . Як і раніше , ,

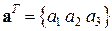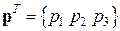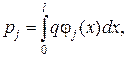
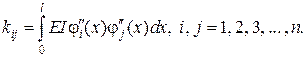
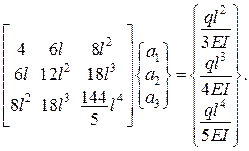
Розв’язок цієї системи дає:

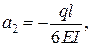
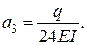
При .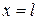

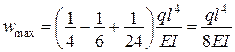Перейдемо безпосередньо до методу Бубнова-Гальоркіна. Нагадаємо, що рівність нулю першої варіації 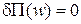, дає

,

,

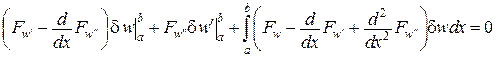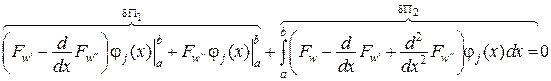
Якщо 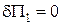, то рівняння 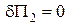дає

,

звідки знаходимо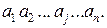

Отримаємо канонічні рівняння методу Бубнова-Гальоркіна для функціонала Лагранжа

.

.

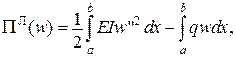
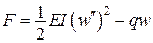
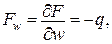
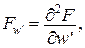
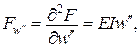
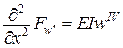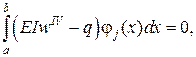
Система алгебраїчних рівнянь

,

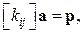
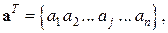
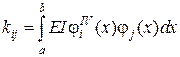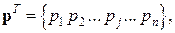
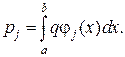
Прикладза методом Бубнова-Гальоркіна.

Оскільки прийнятий вираз 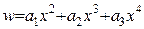не задовольняє усім граничним умовам, зокрема, умовам на правому кінці балки при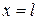 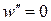і 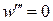, необхідно застосовувати узагальнений метод Бубнова–Гальоркіна, або заздалегідь задовольнити ці граничні умови.

Система рівнянь

,

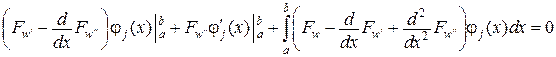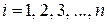
при

, ,

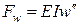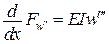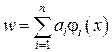
дає такі вирази для коефіцієнтів матриці жорсткості для узагальненого методу Бубнова–Гальоркіна, які співпадають з такими, що отримані за методом Рітца

.

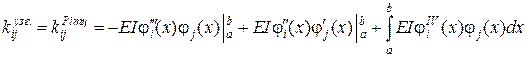Вектор навантажень .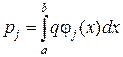

Інтегральні члени, природно, співпадають з коефіцієнтами (♦), а позаінтегральні ураховують граничні умови. Наприклад, 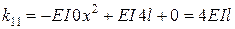і т.д.

Якщо скористатись звичайним підходом Бубнова–Гальоркіна, отримаємо:

.

,

, ,

,

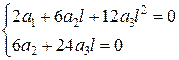
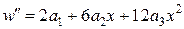
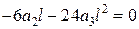
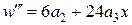
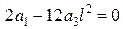
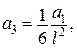
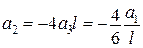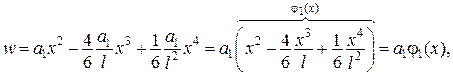
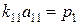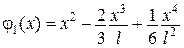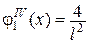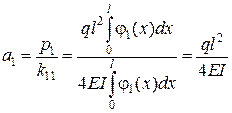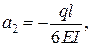
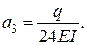
Лекція 12