Основні припущення будівельної механіки
Розрахунки в будівельній механіці базуються на деяких припущеннях. Вони, як правило, збігаються з припущеннями, які мають місце в опорі матеріалів і в теорії пружності, але мають бути віднесені до всієї споруди в цілому.
· Гіпотеза суцільності - тіло вважається суцільним, таким, що неперервно заповнює свій об’єм. На цій підставі деформації і переміщення точок елемента можуть вважатися неперервними функціями координат.
· Гіпотеза однорідності та ізотропності: властивості матеріалу однакові в усіх точках і по усіх напрямках.
· Гіпотеза ідеальної пружності: матеріал конструкцій вважається ідеально пружним. Це означає, що після зняття навантаження деформація усувається, споруда сповна поновлює форму, яку мала до початку навантаження і повертає енергію, яку було витрачено на її деформацію.
· Гіпотеза лінійної залежності між деформаціями і напруженнями:вважається, щоміж напруженнями і деформаціями в усіх точках зберігається лінійна залежність (закон Гука). Завдяки цій гіпотезі, разом з попередніми, пружні властивості матеріалу в усіх точках тіла характеризуються трьома параметрами: модулем пружності E, модулем зсуву G і коефіцієнтом Пуассона n, які пов’язані між собою залежністю 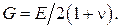
·  Гіпотеза малих переміщень: переміщення точок системи, які зумовлені пружними деформаціями, є малими, тобто такими, що допускають лінійну залежність між деформаціями і переміщеннями в рівняннях геометричного аспекту задачі, а також складання рівнянь рівноваги для недеформованого стану.
Гіпотеза малих переміщень: переміщення точок системи, які зумовлені пружними деформаціями, є малими, тобто такими, що допускають лінійну залежність між деформаціями і переміщеннями в рівняннях геометричного аспекту задачі, а також складання рівнянь рівноваги для недеформованого стану.
Наприклад, якщо елемент AB (рис. 14.1) після деформації займає положення 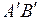 , то лінійна деформація
, то лінійна деформація 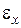 може бути обчислена в такий спосіб:
може бути обчислена в такий спосіб:
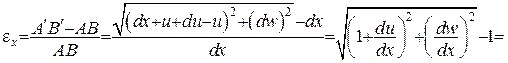
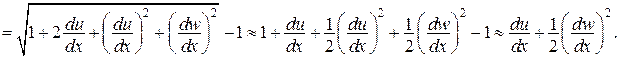
Якщо переміщення малі, такі, що
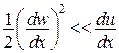 ,
,
то
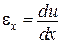
і залежність між деформацією 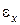 і переміщенням u є лінійною.
і переміщенням u є лінійною.
В опорі матеріалів при розгляді елементарної теорії згину балок гіпотеза малих переміщень дозволяє отримати точне рівняння згину балки.
Загалом, у нелінійній теорії пружності доводиться, що використання лінійних виразів для компонентів деформації можливо лише за виконання двох умов:
1) подовження, зсуви і кути повороту повинні бути малі порівняно із одиницею;
2) квадратичні комбінації кутів повороту повинні бути малі порівняно з відповідними компонентами деформації.
Це дає можливість суттєво спростити розрахунки споруд і вести їх за так званою недеформованою розрахунковою схемою.
На рисунку, наведеному нижче, як приклад, показана деформація тонкого консольного стержня при постійному по довжині згинальному моменті за нелінійною із використанням рівняння (1.1) і лінійною («пунктир»), рівняння (1.2) теоріями. У першому випадку при сталій кривизні стержень згинається по дузі кола, у другому – по параболі. Точний розв’язок для такого стержня при умові нерозтяжності вісі, отриманий з використанням залежностей має вигляд
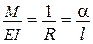 ,
,
відповідно при 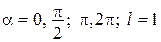 .
.
Нелінійні компоненти переміщень:
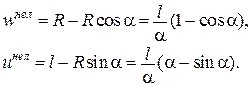
З використанням розкладів тригонометричних функцій у ряди
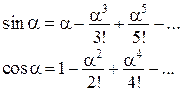
ці розклади з урахуванням 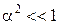 можуть бути спрощені, а саме
можуть бути спрощені, а саме
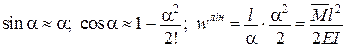 і
і 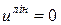 .
.
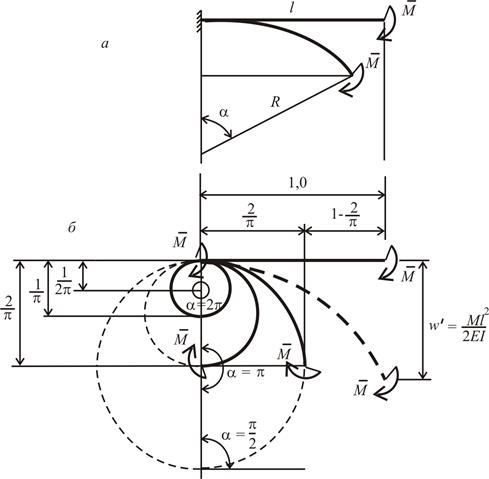
Рис. 14.2

Загальна нелінійна теорія і розрахунки гнучких пружних стержнів викладена в [???].
Зазначимо, що оскільки залежність М і 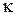 є лінійною (
є лінійною ( 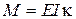 ), то, як і вище, можна отримати варіаційні постановки і для задачі.
), то, як і вище, можна отримати варіаційні постановки і для задачі.
Функціонал Лагранжа
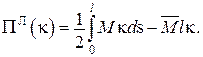 Додаткові умови:
Додаткові умови:
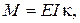
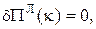
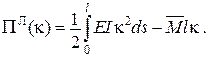
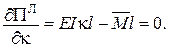
| Функціонал Кастільяно
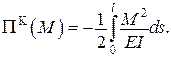 Додаткові умови:
Додаткові умови:
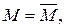
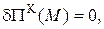
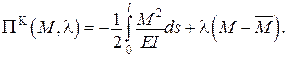
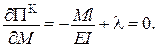
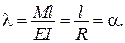
|
Рівняння рівноваги:
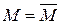
| Рівняння сумісності деформацій:
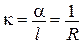 . .
|
| Перші похідні | |
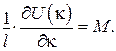
| 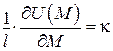 . .
|
| Другі похідні | |
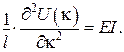
| 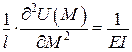 . .
|
Дата добавления: 2016-12-26; просмотров: 1259;
