Принцип двоїстості. Приклади

Згідно з принципом двоїстості матриці рівнянь статичної сторони задачі (рівнянь рівноваги) і геометричної сторони задачі (рівнянь сумісності деформацій) є взаємно транспонованими. Покажемо це на прикладі (рис. 13.1).

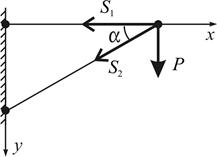Рис. 13.1

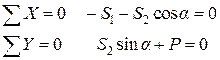
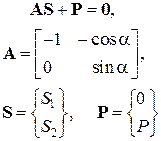
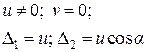
Рис. 13.2

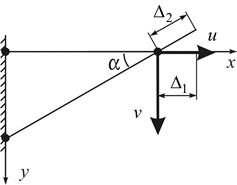Рис. 13.3

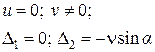
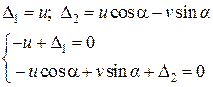
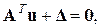
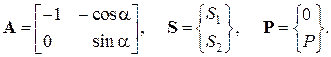
Рівняння плоскої задачі теорії пружності.

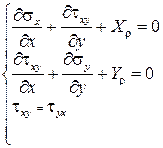
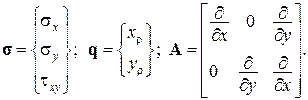
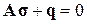– рівняння рівноваги.

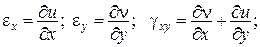
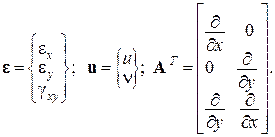
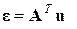– рівняння сумісності деформацій.

Таким чином, у плоскій задачі теорії пружності матриця рівноваги і матриця сумісності деформацій є транспонованими.

Для стержневої системи

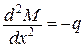– рівняння рівноваги;

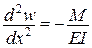– рівняння сумісності деформацій.

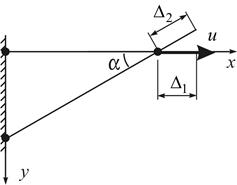
Наслідком принципу двоїстості є те, що матриця жорсткості і матриця піддатливості є взаємно оберненими. Розглянемо наступний приклад (рис. 13.4).

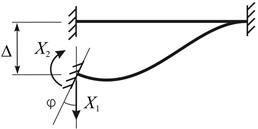Рис. 13.4

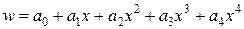
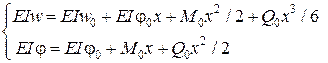
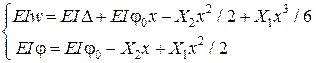
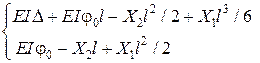
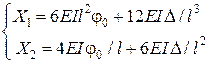- рівняння методу переміщень.

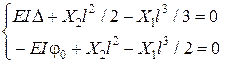
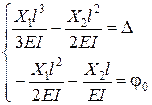- рівняння методу сил.

,

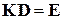де 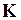- матриця жорсткості; 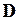- матриця піддатливості.

.

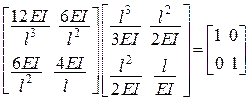Таким чином, матриця жорсткості і матриця піддатливості є взаємно оберненими.

Лекція 14

Поняття про нелінійні задачі