Прямі методи варіаційного числення. Поняття про прямі методи. Принципові схеми методу Рітца, узагальненого методу Бубнова-Гальоркіна, методу Бубнова-Гальоркіна, методу Треффца

Поняття про прямі методи.

1) ,

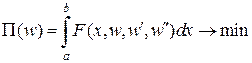
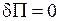2) ,

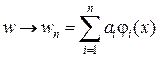де 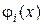– відомі функції, які задовольняють певним умовам, наприклад, граничним, 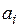– невідомі .

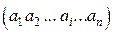3) ,

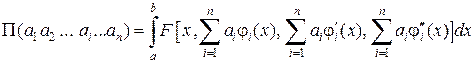4) , , .

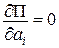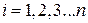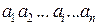Суть прямих методів варіаційного числення полягає у тому, що за допомогою розкладу 2) задача про екстремум функціонала 1) зводиться до задачі про екстремум функції багатьох змінних 3), яка розв’язується традиційним методом 4) і призводить до системи алгебраїчних рівнянь відносно невідомих 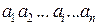, а потім здійснюється граничний перехід до вихідної задачі.

Основні підходи прямих методів.

, .

,

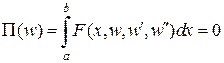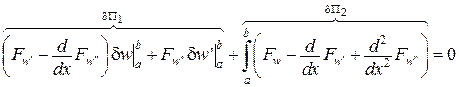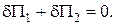
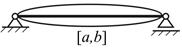
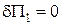
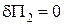
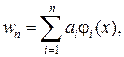
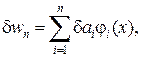
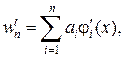
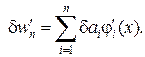
I.w обрані таким чином, що не усі граничні умови задовольняються:

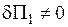
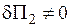
Тоді застосовується звичайна процедура методу Рітца:

1.1 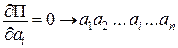, або у розгорнутому вигляді

1.2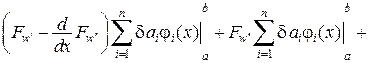

,

(♦)

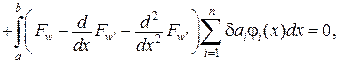
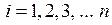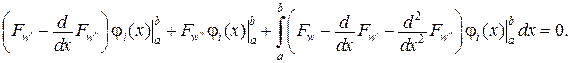Таким чином, отримали вираз (♦), який являє собою систему алгебраїчних рівнянь, після розв’язку яких знаходимо невідомі a₁,a₂, ... a_i … a_n, які містяться у виразах для відповідних похідних , .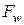

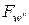Наприклад, якщо

, , ,

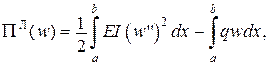
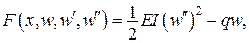
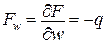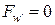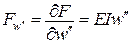а

, .

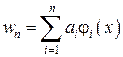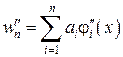Такий підхід має назву узагальненого методу І.Г.Бубнова-Б.Г.Гальоркіна.

II. 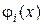підібрані таким чином, що усі граничні умови задовольняються, тоді:

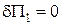, а вираз 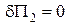дає систему алгебраїчних рівнянь:

,

,

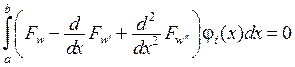з якої знаходяться невідомі коефіцієнти a₁,a₂, ... a_i … a_n.. Такий підхід має назву методу І.Г.Бубнова - Б.Г.Гальоркіна.