Приклади нелінійних задач
 Розглянемо задачу, наведену у [???], яка тлумачиться як «виключний випадок» у тому розумінні, що теорема Кастільяно не дає належного результату, коли переміщення не пропорційні силам. Проте автор при застосуванні теореми Кастільяно не використовує поняття додаткової потенціальної енергії, а помилково користується величиною потенціальної енергії пружної деформації, вираженою через сили.
Розглянемо задачу, наведену у [???], яка тлумачиться як «виключний випадок» у тому розумінні, що теорема Кастільяно не дає належного результату, коли переміщення не пропорційні силам. Проте автор при застосуванні теореми Кастільяно не використовує поняття додаткової потенціальної енергії, а помилково користується величиною потенціальної енергії пружної деформації, вираженою через сили.
Відносна подовжена деформація 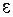 дорівнює
дорівнює
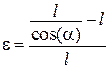 .
.
Ураховуючи, що
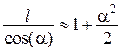 ,
, 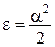 .
.
Відповідно
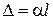 .
.
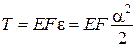 ;
; 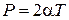 ,
,
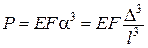 ;
; 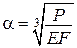 ,
, 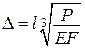 .
.
Для окремого стержня AC1 маємо залежності:
 переміщення
переміщення 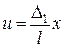 ,
,
деформації 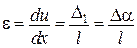 ,
, 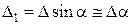 .
.
Рівність варіацій робіт внутрішніх і зовнішніх сил
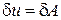
дає
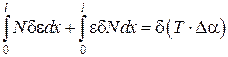 ,
,
або, ураховуючи рівняння рівноваги 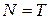 .
.
Зазначимо, що задача є фізично лінійною і тому залежності 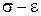 і, відповідно,
і, відповідно, 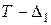 є лінійними (рис. 14.6).
є лінійними (рис. 14.6).
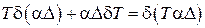 ,
,
але з рис. 14.4
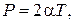
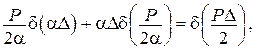
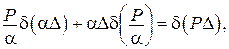
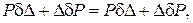
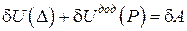
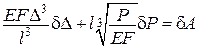 ,
,
або

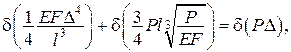
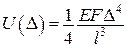 ;
; 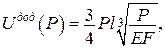
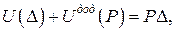
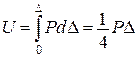 ;
; 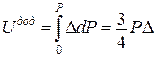 .
.
Рівність
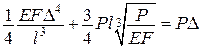 (♦)
(♦)
 є перетворенням Лежандра, а функції
є перетворенням Лежандра, а функції 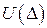 і
і 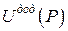 є двоїстими за Юнгом (рис. 14.8).
є двоїстими за Юнгом (рис. 14.8).
Наприклад,
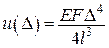 ,
,
тоді
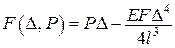 ,
,
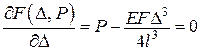 ,
,
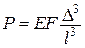 ,
,
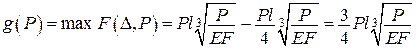 .
.
Відповідно, теореми Лагранжа і Кастільяно дають
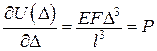 ;
; 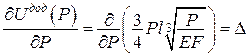 .
.
Згідно з теоремою Донкіна, якщо 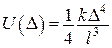 , а
, а 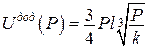 ,
, 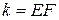
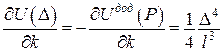 .
.
Зазначимо, що для лінійних задач, значення квадратичної форми 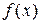 і її перетворення Лежандра
і її перетворення Лежандра 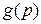 у відповідних точках співпадають
у відповідних точках співпадають 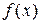 =
= 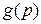 .
.
Для форми 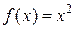 це являє собою відому властивість дотичної до параболи.
це являє собою відому властивість дотичної до параболи.
Загалом це можна довести наступним чином. За теоремою Ейлера про однорідні функції
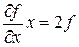 .
.
Тому
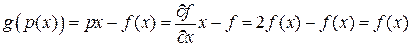 .
.
 Причому
Причому
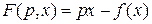 ,
,
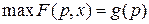 ,
,
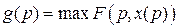 .
.
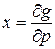 ;
; 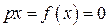 ;
; 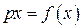 ;
;
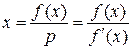 .
.
Координату точки 1 знаходимо із умови
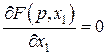 ;
; 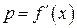 ;
; 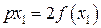 ;
;
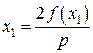 .
.
Координату точки 2 знаходимо із умови
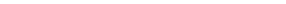
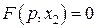 ;
; 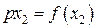 ;
; 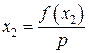 .
.
Якщо 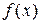 - однорідна квадратична форма, тобто
- однорідна квадратична форма, тобто 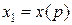 є вісь симетрії.
є вісь симетрії.
Наприклад, у випадку одновісного розтягу (рис.14.4) відповідні перетворення Лежандра мають вигляд
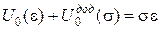 ;
; 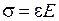
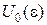 ,
, 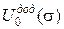 - двоїсті за Юнгом функції.
- двоїсті за Юнгом функції.
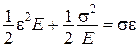 ,
,
або, ураховуючи, що

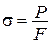 ;
; 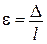 ,
,
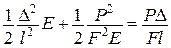 ,
,
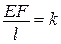 ,
, 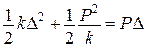 ,
, 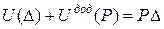 ,
,
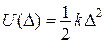 і
і 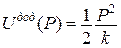 - двоїсті за Юнгом функції, які являють відповідно потенціальну енергію пружної деформації і додаткову потенціальну енергію.
- двоїсті за Юнгом функції, які являють відповідно потенціальну енергію пружної деформації і додаткову потенціальну енергію.
Перетворення Лежандра (рис. 14.11)
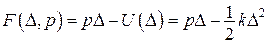 ,
,
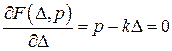 ;
; 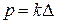 ,
,

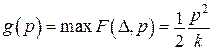 .
.
Функція 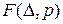 являє собою функціонал Лагранжа
являє собою функціонал Лагранжа 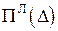 , або повну потенціальну енергію системи (із зворотнім знаком), на графіку
, або повну потенціальну енергію системи (із зворотнім знаком), на графіку 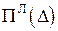 показаний суцільною лінією.
показаний суцільною лінією.
Ділянка 0-1 цієї лінії відповідає навантаженню системи ( 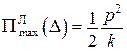 – додаткова потенціальна енергія або робота внутрішніх сил), а ділянка 1-2 – розвантаженню, тобто приведенню системи у первісний стан. Вісь О–О
– додаткова потенціальна енергія або робота внутрішніх сил), а ділянка 1-2 – розвантаженню, тобто приведенню системи у первісний стан. Вісь О–О 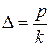 ; яка є умовою перетворення Лежандра, є віссю симетрії. У загальному випадку це має місце для так званих лінійних систем, двоїсті функції яких рівні і ???.
; яка є умовою перетворення Лежандра, є віссю симетрії. У загальному випадку це має місце для так званих лінійних систем, двоїсті функції яких рівні і ???.
Якщо, наприклад, 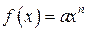 (рис. 14.12), то можна отримати
(рис. 14.12), то можна отримати
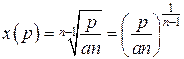 ,
,
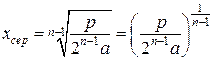 ,
,
де 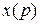 – координата екстремуму, а
– координата екстремуму, а 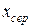 – координата середини.
– координата середини.
 Порівнюючи ці залежності, тобто криві
Порівнюючи ці залежності, тобто криві 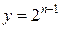 і
і 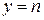 (рис. 14.13), можна отримати:
(рис. 14.13), можна отримати:
1. 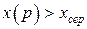 , якщо
, якщо 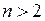 ;
;
2. 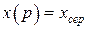 , якщо
, якщо 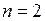 ;
;
3. 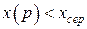 , якщо
, якщо 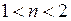 .
.
Ураховуючи, що
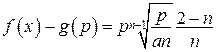 ,
,
послідовно отримаємо:
1. 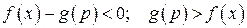 , якщо
, якщо 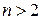 ;
;
2. 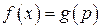 , якщо
, якщо 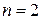 ;
;
3. 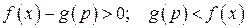 , якщо
, якщо 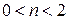 .
.
 Проілюструємо ці положення на подальших прикладах нелінійних задач.
Проілюструємо ці положення на подальших прикладах нелінійних задач.
Функціонал Лагранжа задачі являє собою функцію (рис. 14.14)
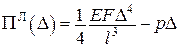 ,
,
екстремум якої послідовно дає
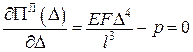 ;
; 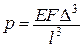 ;
; 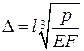 ,
,
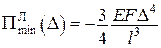 .
.
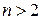
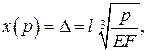
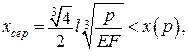
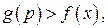
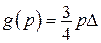 ;
; 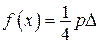 .
.
 Зазначимо, що у випадку нелінійної задачі крива
Зазначимо, що у випадку нелінійної задачі крива 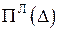 не є симетричною відносно вісі
не є симетричною відносно вісі 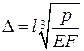 у зв’язку з нелінійною залежністю
у зв’язку з нелінійною залежністю 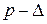 (рис. 14.15). Наприклад, зменшення вдвічі
(рис. 14.15). Наприклад, зменшення вдвічі 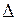 вимагає відповідне зменшення
вимагає відповідне зменшення 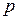 у 8 разів.
у 8 разів.
 Як приклад, розглянемо наступну нелінійну задачу [Варвак], де задана залежність
Як приклад, розглянемо наступну нелінійну задачу [Варвак], де задана залежність 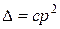 , яка має опуклість, протилежну порівняно із розглянутою вище (рис. 14.16). Необхідно побудувати перетворення Лежандра і функціонал Лагранжа.
, яка має опуклість, протилежну порівняно із розглянутою вище (рис. 14.16). Необхідно побудувати перетворення Лежандра і функціонал Лагранжа.
Тоді:
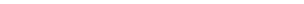
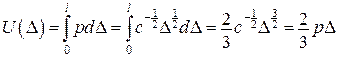 ,
,
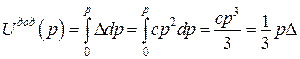 ,
,
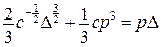 (рис. 14.17).
(рис. 14.17).
Справді, згідно з перетворенням Лежандра
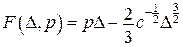 ,
,
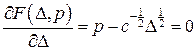 ,
,
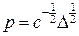 ,
, 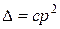 ,
,
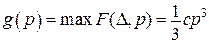 .
.
Відповідно, теореми Лагранжа і Кастільяно дають
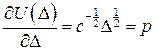 ;
; 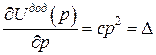 .
.
Згідно з теоремою Донкіна
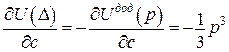 .
.
 Функціонал Лагранжа задачі являє собою функцію (рис. 14.18)
Функціонал Лагранжа задачі являє собою функцію (рис. 14.18)
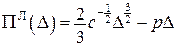 ,
,
екстремум якої дає
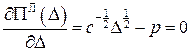 ;
; 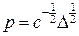 ;
;
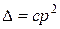 .
.
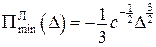 ;
;
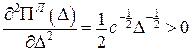 – мінімум,
– мінімум,
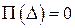 ;
; 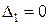 ;
; 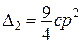 .
.
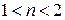 і
і 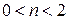
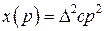 ,
,
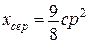 ,
,
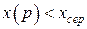 ,
, 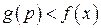 ,
,
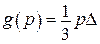 ,
, 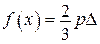 .
.
 Тобто, у даному випадку нелінійної задачі крива
Тобто, у даному випадку нелінійної задачі крива 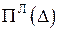 теж не є симетричною відносно вісі
теж не є симетричною відносно вісі 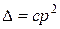 у зв’язку з нелінійною залежністю
у зв’язку з нелінійною залежністю 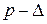 , проте характер зміщення екстремуму протилежний, що пояснюється опуклістю кривої
, проте характер зміщення екстремуму протилежний, що пояснюється опуклістю кривої 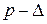 (рис. 14.19).
(рис. 14.19).
Рекомендована література
1. Абовский Н.П., Андреев Н.П., Деруга А.П. Вариационные принципы теории упругости и теории оболочек. - М., 1978. - 287с.
2. Александров А.В., Лащенников Б.Я., Шапошников Н.Н. Строительная механика. Тонкостенные пространственные системы. М, 1983, с. 140-237.
3. Александров А.В., Потапов В.Д. Основы теории упругости и пластичности. М, 1990, с.25-68.
4. Алексеев В.М., Тихомиров В.М., Фомин С.В. Оптимальное управление. М, 1979, с. 11-43.
5. Аппель П. Руководство теоретической (рациональной) механики, том 1. М, 1911.
6. Арнольд В.И. Математические методы классической механики. – М, Наука, 1989.
7. Бабенко А.Є., Бобир М.І., Бойко С.Л., Боронко О.О. Теорія пружності. Частина 1. – К.: «Основа», 2009.
8. Баженов В.А., Богуцкий О.А., Гоцуляк Е.А. Расчет тонких пластин, односторонне опертых по контуру. В сб. «Сопротивление материалов и теория сооружений», вып. 59, К. Будівельник, 1991, с. 3-10.
9. Баженов В.А., Гоцуляк Е.А., Богуцкий О.А. Численная реализация метода квадратичного программирования для расчета стержневых конструкций, односторонне взаимодействующих с упругим основанием. В сб. «Сопротивление материалов и теория сооружений», вып. 58, К., Будівельник, 1991, с. 3-8.
10. Баженов В.А., Гоцуляк Е.А., Кондаков Г.С., Оглобля А.И. Устойчивость и колебания деформируемых систем с односторонними связями, К. – Высшая школа, 1989.
11. Баженов В.А., Гранат СЛ., Шишов О.В. Будівельна механіка. - Київ, 1999. 584 с.
12. Баженов В.А., Дехтярюк Е.С. Будівельна механіка. Динаміка споруд. Київ, 1998, 207 с.
13. Баженов В.А., Дехтярюк Є.С. Імовірнісні методи розрахунку конструкцій. Випадкові коливання пружних систем. – К.; ВІПОЛ, 2005.
14. Баженов В.А., Іванченко Г.М., Шишов О.В. Будівельна механіка. Розрахункові вправи. Задачі. Комп’ютерне тестування. – К: Каравела, 2007.
15. Баженов В.А., Криксупов Е.З., Перельмутер А.В., Шишов О.В. Інформатика. Інформаційні технології в будівництві. Системи автоматизованого проектування. – К, Каравела, 2004.
[1] Важко сказати, коли вперше була висловлена думка про найбільшу «місткість» кола і сфери серед всіх замкнених кривих однакової довжини, або поверхонь однакової площі. Один з останніх учнів афінської школи платоніків Симпліций (VI ст. н. е.), що склав незадовго до остаточного краху античної цивілізації великий коментар до праць Арістотеля (IV ст. до н. е.), пише: «Доведено до Арістотеля, бо він користується цим, як відомим, а потім більш повно – Архімедом і Зенодором, що серед ізопериметричних фігур найбільш містким є коло, а серед ізопіфанних – куля». У цих словах визначена постановка таких екстремальних задач: серед плоских замкнених кривих, що мають задану довжину, знайти криву, яка охоплює найбільшу площу, і серед просторових замкнених поверхонь, що мають задану площу, знайти поверхню, яка охоплює найбільший об'єм. Для філософа-платоніка така постановка задачі є природною і пов'язана з пошуком ідеальних форм. Недаремно коло і куля були в давнину символами геометричної досконалості.
[2] Прозаїчніше мотивування ізопериметричної і близьких до неї задач можна знайти в дещо наївній, але достатньо виразній формі в легенді про Дідону. Нагадаємо її за «Енеїдою» римського поета Вергілія. Фінікійська царівна Дідона із невеликим загоном жителів міста Тіра, рятуючись від переслідувань тирана – брата Дідони, покинули рідне місто і відправилися на кораблях на захід вждовж берегів Середземного моря. Вибравши на африканському узбережжі зручне місце (нинішня Туніська затока), Дідона і її супутники вирішили заснувати тут поселення. Мабуть, ця ідея не сподобалася місцевим жителям, але Дідоні вдалося умовити їх предводителя Ярба, і він необережно погодився поступитися клаптиком землі, «який можна оточити бичачою шкурою». Ярб не відразу зрозумів хитрість і підступність фінікіянки. Розрізавши шкуру на тонкі смужки, Дідона зв'язала їх в один довгий ремінь і, оточивши їм значну територію, заклала на ній місто Карфаген (фінікійське Картадашт – нове місто). На згадку про цю історію цитадель Карфагена дістала назву Бірса (мовою пунійців, так римляни називали жителів Карфагена, – шкура). Цією назвою послуговуються і досьогодні. Всі ці події легенда відносить до 825 (або до 814) р. до н.е.
У такій ситуації виникає та ж сама класична ізопериметрична задача: вказати оптимальну форму ділянки землі, яка при заданій довжині периметра L має найбільшу площу S. Її розв’язком є коло. Інші постановки задачі можна отримати якщо, як це природно припустити, Дідона хотіла зберегти вихід до моря. На відміну від класичної ізопериметричної задачі, ці задачі будемо називати задачами Дідони.
[3] Перший загальний аналітичний прийом розв’язання екстремальних задач розроблений П’єром Ферма. Відкритий він, мабуть, у 1629 р., але вперше достатньо повно викладений в листі до Роберваля у 1638р. Щоб осягнути первинну думку Ферма можна звернутися до книги Декарта, де цей лист наведений. (Р. Декарт. Геометрія. З додатком вибраних робіт П. Ферма і листування Декарта. − М. − Л.: ГОНТІ, 1938, с. 154). Сучасною мовою (правда, у Ферма лише для поліномів) прийом Ферма зводиться до того, що при знаходженні екстремуму функції 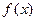 без обмежень в точці екстремуму
без обмежень в точці екстремуму 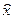 має виконуватися рівність
має виконуватися рівність 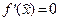 . Відомо, що перший натяк на цей результат з’явився в словах Кеплера із «Стереометрії винних бочок».
. Відомо, що перший натяк на цей результат з’явився в словах Кеплера із «Стереометрії винних бочок».
Точного сенсу міркування Ферма набули через 46 років, коли у 1684 р. з'явилася робота Лейбніца, в якій закладалися основи математичного аналізу. Вже сам заголовок цієї роботи, який починається так: «Nova methodus pro maximis et minimis...» («Новий метод знаходження найбільших і найменших значень...»), свідчить про важливість задачі знаходження екстремумів в становленні сучасної математики. У своїй статті Лейбніц не тільки отримує як необхідну умову співвідношення 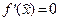 (цей результат зараз називають теоремою Ферма),але і використовує другий диференціал для розрізнення максимуму і мінімуму. Слід зазначити, що більшість наведених Лейбніцем фактів на той час були відомі також і Ньютону. Проте його робота «Метод флюксій», завершена в основному до 1671 р., була опублікована тільки у 1736 р.
(цей результат зараз називають теоремою Ферма),але і використовує другий диференціал для розрізнення максимуму і мінімуму. Слід зазначити, що більшість наведених Лейбніцем фактів на той час були відомі також і Ньютону. Проте його робота «Метод флюксій», завершена в основному до 1671 р., була опублікована тільки у 1736 р.
[4] Лагранж Жозеф Луі (фр. Joseph Louis Lagrange, італ. Giuseppe Lodovico Lagrangia; 1736 - 1813) — французський математик, астроном і механік італійського походження. Народився в Турині. Вчився у Туринському університеті. Дослідження присвячені механіці, геометрії, теорії диференціальних рівнянь, математичному аналізу, алгебрі, теорії чисел та іншим розділам математики, а також теоретичній астрономії. В роботі „Аналітична механіка” (1788) Лагранж підвів підсумок усьому, що було зробленоу механіці протягом XVIII ст. і завершив математизацію механіки. В основу статики він поклав принцип можливих переміщень, а в основу динаміки – поєднання принципу можливих переміщень з принципом Д’Аламбера. У роботах „Теорія аналітичних функцій” (1797) і „Лекції по численню функцій” (1801) зробив спробу обгрунтувати аналіз, зводячи його до алгебри. Запропонував аналітичне викладення варіаційного числення. Виходячи із результатів Л.Ейлера розробив основні поняття варіаційного числення. Ввів потрійні інтеграли. В теорії аналітичних функцій побудував ряд, що носить його ім’я і довів декілька теорем, сформульованих П.Ферма. В механіці і математиці Лагранж виконав роботу з систематизації отриманих результатів і їх обгрунтуванню.
[5] Дю-Буа-Реймонд, Поль Давид Густав (нім. Paul David Gustav du Bois-Reymond, 1831–1889) – німецький математик. Його ім'ям названа одна з лем варіаційного числення.
[6] Пуассон, Сімеон Дені (фр. Siméon-Denis Poisson, 1781 — 1840) – французький математик, механік і фізик, один із засновників математичної фізики. Дослідження присвячені варіаційному численню, теорії ймовірності, математичній фізиці, механіці, зокрема, теорії пружності, опору матеріалів. Написав «Курс механіки» (1811), який багато разів перевидавався.
[7] В цьому функціоналі знак змінений на зворотній порівняно з традиційною формою функціонала Кастільяно з тим, щоб витримати принцип двоїстості за Юнгом у нерівності Лежандра. Тобто прийнято, що відповідні значення функціоналів 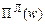 і
і 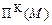 будуть співпадать, оскільки вони є квадратичними формами.
будуть співпадать, оскільки вони є квадратичними формами.
Дата добавления: 2016-12-26; просмотров: 865;
