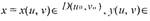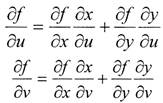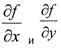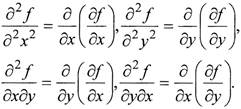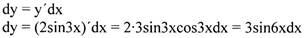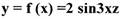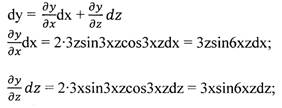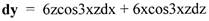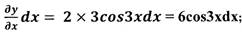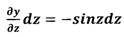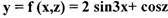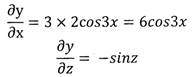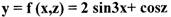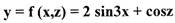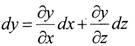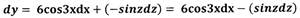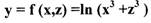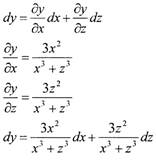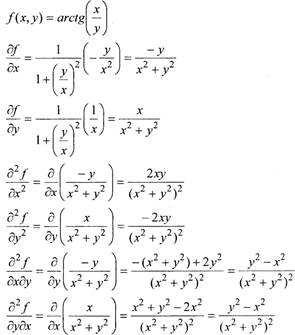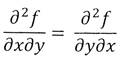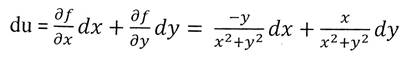2 страница. Задача/. Составить уравнение касательной и/или нормали к кривой точке с абсциссой х0.
Задача/. Составить уравнение касательной и/или нормали к кривой
точке с абсциссой х0.
решение
Если функция f(x) в точке х0 имеет конечную производную, то уравнение касательной имеет вид
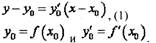
|
, то уравнение касательной имеет вид то уравнение нормали имеет вид
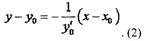
|
| то уравнение нормали имеет вид
|
| Задача 3: Найти уравнение касательной к параболе
|
| решение
Будем искать уравнение касательной в виде уравнения прямой с угловым коэффициентом, т.е. у = kx + b. Известно, что к есть тангенс угла наклона прямой к положительному направлению оси ОХ, т.е. k = у'(М1). Так как М1 принадлежит и касательной и параболе, то ее координаты удовлетворяют их уравнениям.
|
Задача 2. Составить уравнение нормали к данной кривой в точке с абсциссой
решение
Имеем:
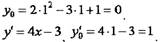
|
• Получаем уравнение нормали:
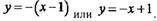
|
• Составляем уравнение касательной к данной кривой в точке с
абсциссой х0).
Имеем:
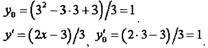
|
• Получаем уравнение касательной:
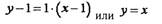
|
В точке М1
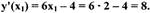
|
Подставив x1 = 2 в уравнение параболы, найдем ординату у1 точки М1:
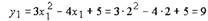
|
Значит k = 8. Подставив значение k = 8;
x1= 2; y1 = 9 в уравнение прямой, найдем b: 9 = 8 • 2 + b; b = - 7.
Значит касательная к параболе у = Зх2 - 4х + 5 в точке М1 (2,9) будет
представлена уравнением у = 8х — 7.
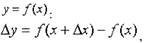 может быть представлено в
может быть представлено в
|
| то соответствующее приращению аргумента
|
Определение 3. Если приращение функции
| называется дифференцируемой в точке х.
|
| бесконечно малая более высокого порядка малости, чем
|
| Таким образом, существование
|
| в точке х эквивалентно её
|
производной у функции
дифференцируемости в этой точке по определению 3.
Определение 4. Главная линейная часть приращения дифференцируемой
| называется ее дифференциалом.
|
ДИФФЕРЕНЦИАЛ ФУНКЦИИ И ДИФФЕРЕНЦИАЛ
АРГУМЕНТА
| является функцией двух аргументов -
|
независимой переменной совпадает с ее приращением). Дифференциалы
старших порядков определяются индуктивно.
По определению производной
получим:
где — бесконечно малая величина (БМВ) при х = 0. Умножая обе части
(1) на Δх, получим:
где Δх при х = 0 тоже БМВ.
Лейбниц предложил обозначить
и назвать это дифференциалом функции. Тогда, если у = х, то
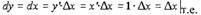
|
Откуда дифференциал аргумента dx равен приращению аргумента —
Δх. Можно (4) представить в виде:
| • Пример. Найти дифференциал функции
|
Решение: По формуле (6) получим:
Отсюда формулами для нахождения дифференциала будут формулы
для нахождения производной, где вместо знака производной перед
функцией будет стоять символ d.
Например:
| считается функцией только х (но не
|
этом
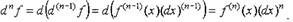 Соотношение
Соотношение
|
| выполняется, например, для n-1=1.
|
| Методом индукции из этого следует справедливость аналогичного выражения для n-го дифференциала при любом n ≥ 2 .
|
Определение. Дифференциалом п-го порядка функции
называется дифференциал от (n-1)-го дифференциала этой функции. При
• Пример. Вычислить 1-й и 2-й дифференциалы функции
Решение:
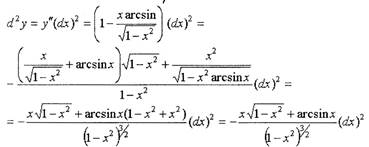
|
ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ДИФФЕРЕНЦИАЛА ФУНКЦИИ
| Подставляя (9) в (2), получим:
|
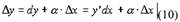 (бесконечно малая величина), предел которой
(бесконечно малая величина), предел которой
|
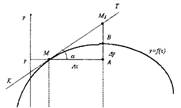
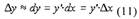 На рис. рассмотрим геометрический смысл выражения (10).
На рис. рассмотрим геометрический смысл выражения (10).
|
С учетом (9) и (11) можно сказать, что
дифференциал функции в конкретной
точке отличается от приращения
функции в этой точке на бесконечно
малую величину, соответствующую
отрезку между точками пересечения
| Понимание геометрического смысла производной
|
вертикальной проекции приращенного аргумента с графиком функции
и с продолжением касательной, проведенной к графику в
рассматриваемой точке.
позволяет определять приближенное значение функции
• Пример 1. Определить приближенное значение
Решение: Рассмотрим функцию
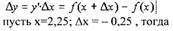
|
| Решение: По условию примера мы имеем:
|
• Пример 2. Найти абсолютную погрешность средней скорости
спринтера в створе двух фотолучевых установок (ФЛУ),
отстоящих друг от друга на расстоянии 5 м, если спринтер
пробегает это расстояние за 0,422 с и ошибка в расстоянии за
счет вертикальных колебаний тела составляет 20 см, а время
определено с ошибкой 0,002 с.
| Дифференциал скорости согласно (41) будет:
|
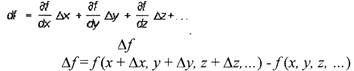
| в случае, когда оно отличается от
|
| на величину, бесконечно малую по сравнению с
|
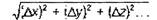 или
или
|
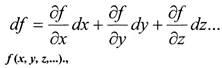
| -полный дифференциал функции
|
ПОЛНЫЙ ДИФФЕРЕНЦИАЛ
Полный дифференциал df, функции f(x, у, z,...) нескольких
независимых переменных - выражение
| - первые частные производные,
|
Дифференциал функции двух переменных.
Определение: Дифференциал df(x0 , y0) функции
называется следующее выражение:
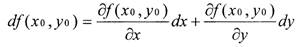
|
| где dx и dy — дифференциалы
|
| или сокращённо: переменных x и y.
|
Следовательно, мы можем представить df в следующем виде:
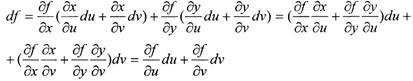
|
Последнее равенство следует из формул замены переменных. Таким образом, df можно представить в виде:
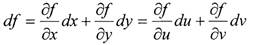
|
Это равенство и выражает свойство инвариантности первого дифференциала.
Дифференцирование сложной функции.
Сложная функция h(x) = g(f(x))
(сложная функция с одной переменной)
Правило дифференцирования сложной функции (Цепное правило) позволяет
вычислить производную композиции двух и более функций на основе
индивидуальных производных. Если функция f имеет производную в точке
х0, а функция g имеет производную в точке у0 = f(x0), то сложная функция
h(x) = g(f(x)) также имеет производную в точке х0.
| представлена в следующем виде:
|
производная сложной функции может быть
Теорема: Пусть
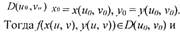
|
Пример (сложная функция с одной переменной)
| Дифференцируя эти функции отдельно:
|
получаем
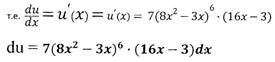 и функции
и функции
|
Частные производные высших порядков
| Первые частные производные
|
| есть функции от переменных х и у.
|
Назовём по определению вторыми частными производными функции следующие выражения:
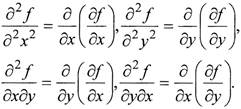
|
Пример: Найти дифференциал функции у = f (х) = 2 sin3x (сложная
функция с одной переменной x)
Решение.
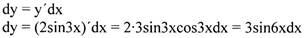
|
Пример: Найти дифференциал функции
функция с двумя переменными: x,z)
Решение.
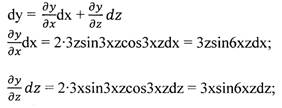
|
Пример: Найти частные производные функции
(функция с двумя переменными: x,z)
Решение.
Пример: Найти частные дифференциалы функции
Решение.
Пример: Найти полный дифференциал функции
Пример: Найти полный дифференциал функции
Решение
Решение
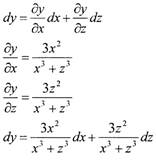
|
Пример: u = f(x,y)
Найти частные производные первого и второго порядка и полный
дифференциал функции u. du -?
Решение
ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ К ИССЛЕДОВАНИЮ ФУНКЦИИ
Возрастание и убывание функции. Экстремум функции.
Определение 1.
Функция f(x) называется возрастающей в интервале (а,b), если при
возрастании аргумента х в этом интервале соответствующие значения
функции f(x) также возрастают, т.е. если
f(x2) >f(x1) при x2 > x1.
Из этого определения следует, что у
возрастающей в интервале (а,b)
функции f(x) в любой точке этого
интервала приращения Δх и Δу
имеют одинаковые знаки.
Дата добавления: 2016-06-24; просмотров: 3816;
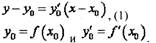
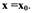
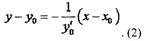
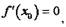
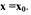
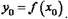
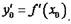
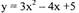
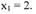
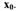
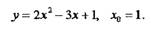
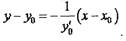
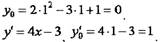
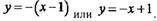
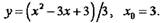
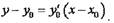
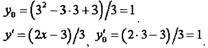
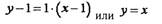
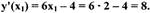
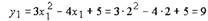
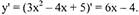
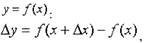 может быть представлено в
может быть представлено в
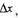
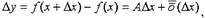
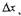
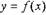
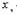
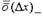
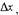
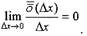
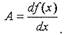
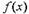
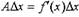
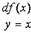
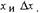

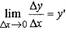
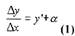
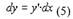
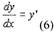
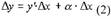
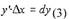
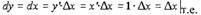
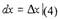
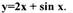
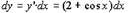
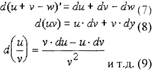
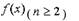
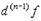
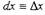
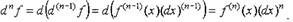 Соотношение
Соотношение
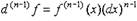
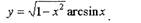
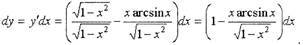
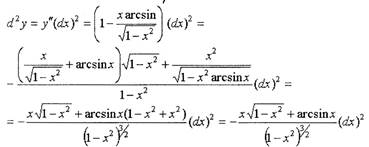
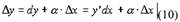 (бесконечно малая величина), предел которой
(бесконечно малая величина), предел которой
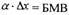
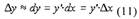 На рис. рассмотрим геометрический смысл выражения (10).
На рис. рассмотрим геометрический смысл выражения (10).
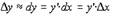
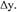
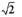
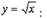
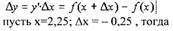
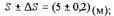
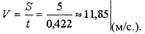
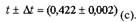
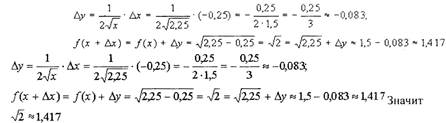
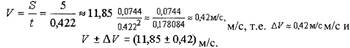
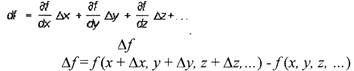
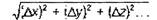 или
или
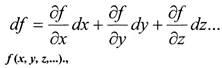
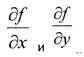
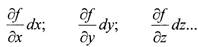
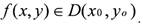
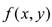
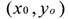
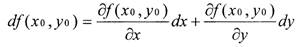
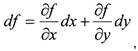
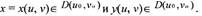
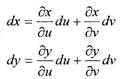
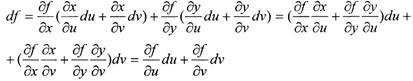
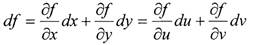
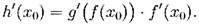
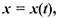
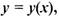
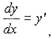
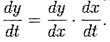
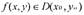
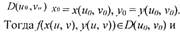
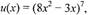
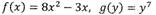
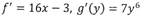
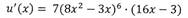
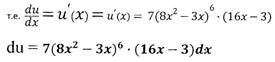 и функции
и функции