Основы геометрии. Линии и углы. Треугольники

Геометрия - раздел математики, изучающий природу линий, точек, поверхностей и тел, пространственные отношения и их обобщения. Геометрию точек, прямых и плоскостей, а также фигур на плоскости и тел в пространстве исследовали еще древние греки.

К примеру, основы элементарной геометрии (планиметрии и стереометрии), ныне изучаемой в средней школе, заложил в III в. до н. э. древнегреческий математик Евклид.

Линии. Линия соединяет две и более точек. Имеет только одно измерение - длину и может быть прямой или кривой. Касательная. Прямая линия, которая соприкасается с окружностью только в одной точке, но не пересекает ее.

Ось, или линия симметрии. Разделяет симметричную фигуру (например, равнобедренный треугольник) на две зеркально отраженные половины.

Параллельные. Две и более линии, расстояние между которыми сохраняется по всей длине, называются параллельными. По соглашению, параллельные линии обозначают знаком «стрелка».

Точка - это положение в пространстве. Она не имеет измерений: ни длины, ни ширины, ни высоты.

Перпендикуляр. Прямую линию, соприкасающуюся с другой линий под прямым углом (90°), называют перпендикуляром ко второй линии.

Углы. Угол - геометрическая фигура, образованная двумя лучами (сторонами угла), выходящими из одной точки (вершины угла). Углы измеряют в градусах (°) (или радианах). Существует шесть основных типов углов:

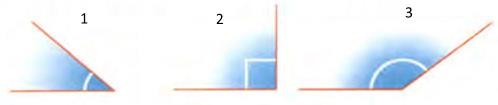
1. Острый угол. Угол, меньший 90°
2. Прямой угол. Точно равен 90°. что отмечают на чертеже небольшим квадратом.
3. Тупой угол. Угол, больший 90° и меньший 180°.

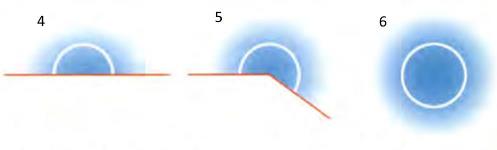
4. Развернутый угол. Точно равен 180°
5. Отраженный угол. Больше 180° и меньше 360°.
6. Полный угол равен 360°.

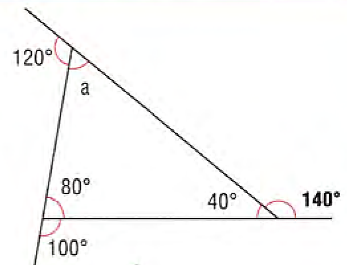
Треугольники. У треугольников три вершины и три стороны. Сумма всех внутренних углов треугольника всегда равна 180° (см. чертеж справа). Различают шесть основных типов треугольников.

1. Равносторонний треугольник. Все три стороны имеют одинаковую длину, каждый внутренний угол равен 60°. Есть три оси симметрии.
2. Равнобедренный треугольник. По крайней мере две стороны одинаковой длины, и не менее двух углов равны между собой. Есть одна ось симметрии.
3. Неравносторонний треугольник. Все три стороны разной длины, и все углы также различны. Осей симметрии нет.

4. Остроугольный треугольник. Все углы - острые (меньше 90°).
5. Прямоугольный треугольник. Один угол равен 90° - прямому углу. Сторона, противоположная этому углу, называется гипотенузой.
6. Тупоугольный треугольник. Один угол тупой (больший 90° и меньший 180°).

Сумма углов. Так как внутренние углы треугольника в сумме всегда дают 180°, можно вычислить неизвестный угол а: 180° - 80° - 40° = 60°. Сумма внешних углов треугольника (140 + 120 + 100) равна 360°.

Четырехугольники. Четырехугольник - плоская фигура, ограниченная четырьмя сторонами (также называют четырехсторонний многоугольник). Сумма внутренних углов четырехугольника всегда 360°. Различают шесть основных типов четырехугольников.

1. Прямоугольник. Четырехугольник, у которого все углы прямые. Противоположные стороны параллельны и равны.
2. Квадрат. Правильный четырехугольник, все углы которого являются прямыми и все стороны равны.
3. Параллелограмм. Четырехугольник у которого противолежащие стороны попарно параллельны, т. есть лежат на параллельных прямых.

4. Ромб. Четырехугольник, у которого все стороны равны, противолежащие стороны попарно параллельны и противоположные углы равны..
5. Трапеция. Четырехугольник, у которого только одна пара противолежащих сторон параллельна. Если боковые стороны равны, то эта трапеция называется равнобедренной.
6. Ромбическая трапеция. Две пары соприкасающихся сторон одинаковой длины. Противоположные углы между этими парами равны. Два других угла не равны.

Круги и кривые. Геометрия изучает также кривые линии и фигуры, как плоские (например, окружности), так и объемные (например, сферы), которые ограничиваются этими линиями. Следующие термины описывают кривые фигуры и их свойства.

1. Круг. Часть плоскости, ограниченная окружностью.
2. Окружность. Линия, отмечающая периметр (границу) круга. Расстояние по периметру называется длиной окружности.
3. Хорда. Отрезок, соединяющий две точки окружности.
4. Диаметр. Хорда, проходящая через центр окружности.
5. Радиус. Отрезок, соединяющий центр окружности с какой-либо ее точкой.
6. Сфера. Тело, ограниченное одной кривой поверхностью, все точки которой равно отстоят от одной точки - центра сферы.

7. Эллипс. Называют также овалом (неточно). Математически эллипс является сечением конуса, которое не проходит через его основание и не параллельно ему.
8. Большая ось. Длинная ось эллипса. Прямая, которая проходит через центр эллипса, разделяет его на две равные половины и соединяет две наиболее удаленные точки его периметра.
9. Малая ось. Короткая ось эллипса. Прямая, которая проходит через центр эллипса, разделяет его на две равные половины и соединяет две наименее удаленные точки его периметра.
10. Эллипсоид. Известен также как «овоид» (неточно). Тело, все сечения которого являются эллипсами или кругами.

Цилиндр. Трубообразное тело с прямыми сторонами и круглое в поперечном сечении.
Конус. Тело, имеющее в основании круг и кривые стороны, сходящиеся в вершине.

Многоугольник - геометрическая фигура, ограниченная тремя и более прямыми линиями. Правильные многоугольники, такие, как квадрат (правильный четырехугольник), имеют одинаковые стороны и равные внутренние углы; неправильные многоугольники, например трапеция (неправильный четырехугольник), имеют разные стороны и углы. Многоугольники называют по числу сторон. Чем больше сторон, тем больше сумма внутренних углов многоугольника, однако сумма его внешних углов (см. «Треугольники», слева) всегда 360°.