Числа и последовательности. Разделы математики. Числа всех видов

Математика - наука о числах, формах и количественных отношениях. Она является составной частью других дисциплин - от физики и биологии до теории управления. Это универсальный инструмент познания мира. Даже в эстетике математика находит свое применение, благодаря «золотому сечению».

Разделы математики. Математика подразделяется на две основные части: теоретическую и прикладную.

Теоретическая математика изучает математические теории безотносительно к какой-либо практической задаче.
Прикладная математика использует математические методы в других областях, включая научные дисциплины, такие, как физика, химия, биология.

Основные разделы теоретической и прикладной математики:
- Алгебра. Использование букв или символов, заменяющих любые неизвестные числа в вычислениях.

- Арифметика. Наука о числах и действиях над ними, включая их сложение, вычитание, умножение и деление.

- Вероятностей теория. Наука о случайных событиях и способах вычисления вероятности, что они произойдут.

- Геометрия. Изучает точки, линии, углы, поверхности и тела, а также отношения между ними.

- Исчисления. Изучение непрерывных изменений, например кривых линий на графике, с помощью алгебры.

- Множеств теория. Множество - любая группа точно определенных элементов, например, все люди старше 50 лет; установлены правила, по которым определяется, принадлежит элемент множеству или нет.

- Статистика. Сбор, обработка и интерпретация числовой информации.

- Тригонометрия. Изучение углов и треугольников, применение этих знаний в геометрии и других областях.

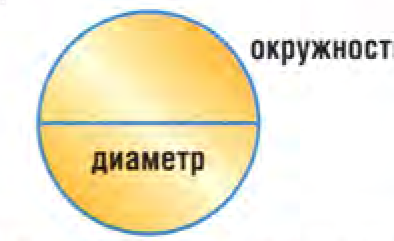
Число Пи. Иррациональное, или неточное, число (см. ниже) π, или «пи», определяется как отношение длины окружности к ее диаметру.

Это одно из наиболее важных чисел в математике, применяемое для вычисления длины кривых, площадей кривых поверхностей и объема тел. Оно даже входит в формулы, описывающие вибрацию струн и движения маятника.

Оно не может быть представлено дробью, хотя неправильная дробь 22/7 иногда используется для выражения его приблизительного значения.

С точностью до первых 120 десятичных знаков его значение равно: 3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986 28034825342117 067982148086513282306647.

Числа всех видов. Самые простые числа - натуральные (или целые) - применяют для подсчета целого количества предметов. Это первые числа, которые заучивают дети: 1, 2, 3, 4, 5, 6, 7 и т.д.

Целые. Эти усовершенствованные натуральные числа используют для счета целых шагов по числовому ряду, вперед и назад, вверх и вниз. Целые - натуральные числа со знаками «плюс» или «минус» перед ними: -7, -6, -5, -4, -3, -2. -1, 0, +1, +2, +3. +4, +5, +6, +7. На практике положительные числа обычно записывают без знака «плюс».

Действительные числа. Все числа, которые существуют: не только целые, но и бесчисленное множество других чисел, лежащих между ними. Они записываются как простые дроби или десятичные: 6,989, 5⁵/₈ и т.д.

Простые числа. Целые числа, которые делятся только на 1 и самих себя. Пример. Первые 20 простых чисел: 1. 2. 3, 5, 7, 11, 13. 17, 19, 23, 29. 31, 37. 41, 43, 47, 53, 59, 61. 67.

Множители. Число, которое делит нацело другое число, - множитель. Пример. Множителями числа 12 являются 1, 2, 3, 4, 6 и 12. Множитель, который одновременно простое число, называется простым множителем. Пример. 2 и 3 - простые множители числа 12.

Совершенные числа. Натуральные числа, которые равны сумме всех своих множителей. Пример. 28 есть совершенное число, поскольку 1,2, 4, 7 и 14 — его множители, а 1 + 2 + 4 + 7 + 14 = 28. Первые шесть совершенных чисел: 6, 28. 496. 8128, 33550336, 8589869065.

Бесконечность. Число, которое слишком велико для счета, находящееся на теоретическом конце ряда действительных чисел. Обозначается символом ?.

Иррациональные числа. Большинство чисел (известные как рациональные) можно выразить точно, используя десятичные или другие дроби. Но точные значения некоторых чисел невозможно записать подобным образом. Они называются иррациональными. Пример, Квадратный корень из 2 - иррациональное число. Его приблизительное значение: 1,4142135623730950488016887242097. Можно добавлять все новые цифры, но значение числа все равно не будет записано точно.

Периодические числа. Некоторые рациональные числа, выраженные как десятичные дроби, имеют бесконечную дробную часть. Пример. Если 1/2 = 0,5, то 1/6 = 0,1666666666666 или 0,1(6) - 6 в периоде. Иногда повторяется группа цифр. Пример. 3/7 = 0.42857 142857 142857 142…

Золотое отношение. Также называется золотым сечением, золотым средним и божественной пропорцией. Представляет собой иррациональное число со значением или приблизительно 1,618034.

Его можно вычислить с помощью последовательности Фибоначчи. Если каждое число в ряду Фибоначчи делить на предшествующее, отношение будет стремиться к приблизительному значению 1,618034.

Числовой ряд. Числа в ряду, показанном выше, - целые. Ряд действительных чисел изобразить невозможно, поскольку он должен включать бесчисленное множество чисел, располагающихся между целыми

Числовые последовательности. Числовые последовательности - организованный набор (множество) последовательных чисел, соответствующих определенным правилам. Простейшую последовательность представляют числа натурального ряда: 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11. Они связаны правилом: «Прибавь единицу к предыдущему числу».

Два простых типа последовательностей - арифметическая и геометрическая прогрессии.

Арифметическая прогрессия. В этой последовательности разность между двумя соседними числами, называемая разностью прогрессии, никогда не изменяется. Пример. Последовательность 4; 6,5; 9; 11,5; 14; 16,5; 19 - возрастающая арифметическая прогрессия с разностью 2,5.

Последовательность 176, 150, 124, 98, 72, 46, 20 есть убывающая прогрессия с разностью 26.

Если известна разность (d) и первый член (а) арифметической прогрессии, можно вычислить любое число в этой последовательности. Чтобы вычислить n-ный, так называемый общий член прогрессии, следует умножить d на (п-1) и прибавить а.

Формула. Значение n-ного члена = а + (n-1)d. Пример. Каково значение 11-го члена последовательности: 6, 10, 14, 18, 22, 26 ...? а = 6 и d = 4 Значение 11 -го члена = 6 + (11 -1) х 4 = 6 + 10x4 = 46.

Геометрическая прогрессия. Каждое число в этой прогрессии умножают на постоянный, характерный для нее множитель, называемый знаменателем прогрессии, чтобы получить следующее число последовательности.

Пример. Последовательность 2, 4, 8, 16, 32, 64. 128, 256 является геометрической прогрессией со знаменателем 2: 2x2 = 4, 2x4 = 8, 2x8 = 16 и т. д.

Чтобы найти n-ное число, или общий член геометрической прогрессии, вычислите (п-1) степень знаменателя (т) и умножьте результат на а (первый член последовательности).

Формула. Значение n-ного члена = = am(n-1). Пример. Каково значение 8-го члена последовательности: 3, 6, 12, 24. 48, 96 ... ? а = 3 и m = 2 Значение 8-го члена = 3 х 2^(8-1) = 3 х 27 (т.е. 2, умноженное само на себя семь раз) = 3 x 128 = 384.

Последовательность Фибоначчи. В ряду чисел, представленных выше, каждое следующее число, или член, образуется путем сложения двух предыдущих: 0 + 1=1, 1+1 =2, 1 + 2 = 3, 2 + 3 = 5, и т. д.

Эта последовательность была открыта математиком Леонардо Пизанским, или Леонардо Фибоначчи (около 1170 - 1240). Столетия спустя было найдено, что она имеет много интересных свойств, имеющих отношение не только к математике, но и к природе, искусству и архитектуре. Она также тесно связана с золотым отношением (см. ниже).

Прямоугольники и спирали. Последовательность Фибоначчи можно выразить не только числами, но и рядом прямоугольников, а также спиралью, нарисованной с их помощью.

В этой форме числа Фибоначчи чаще всего встречаются в природе и в искусстве. Прямоугольники Фибоначчи строятся следующим образом:
- Начертите два маленьких квадрата с размерами сторон 1 единица х 1 единица. Вместе они дадут прямоугольник размером 1 х 2.
- Под этим прямоугольником начертите квадрат 2x2. Вместе они образуют прямоугольник 2x3.
- Справа к полученному прямоугольнику прибавьте квадрат 3x3, что даст прямоугольник 3x5.
- Сверху начертите квадрат 5x5, чтобы получить прямоугольник 5x8 (этот процесс можно продолжать до бесконечности).

Чтобы получить спираль, проведите по четверти окружности в каждом квадрате, начиная с первого. Получившаяся спираль очень напоминает форму раковин некоторых моллюсков, например улиток или наутилуса.

Фибоначчи и золотое отношение. Прямоугольники Фибоначчи обладают некоторыми любопытными свойствами. Например, длина стороны каждого из них равна двум последовательным числам Фибоначчи. Эти прямоугольники заключают в себе золотое отношение. Возьмем прямоугольник 5 X 8, в нем 8 : 5 = 1,6. Следующий прямоугольник будет иметь размеры 8x13: 13 : 8 = 1.625. Чем больше прямоугольников будет добавлено, тем ближе отношение сторон к золотому отношению - приблизительно 1,618034.

Такие пропорции найдены во многих предметах, которые мы находим прекрасными. Древние греки осознавали это - данное отношение часто обнаруживается в архитектуре. Фронтон Парфенона в Афинах, например, есть прямоугольник Фибоначчи, длина фронтона примерно в 1,6 раза больше его высоты.

Фибоначчи в природе и искусстве

Раковина моллюска наутилус (вверху слева) образует спираль Фибоначчи. 8 прямоугольниках (внизу) расстояние от А до С. деленное на расстояние от А до В, равно 1,625 - золотое отношение. На картине Дж. М. Тёрнера точка фокуса - локомотив - лежит на такой же оси.