Перетворення Лежандра

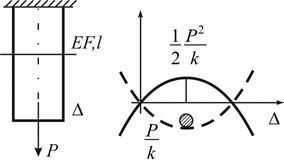Рис. 8.9

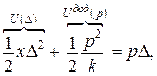
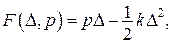
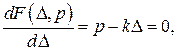
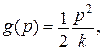
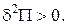
Принцип Лагранжа-Дирихле

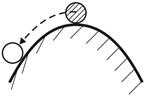
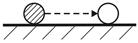
Для консервативної системи стійка, нестійка, байдужа рівновага мають місце відповідно:

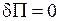
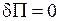
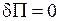
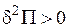
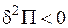
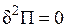
		min max const

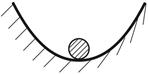
Приклади. Теорема Кастільяно

,

.

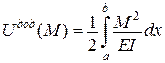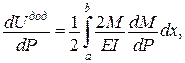
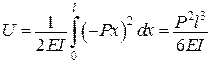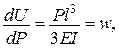
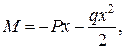
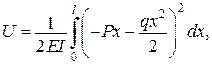
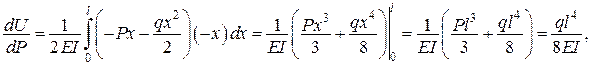
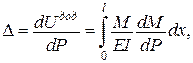
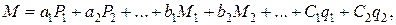
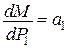, тобто 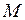при .

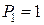
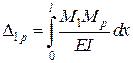Теорема Клапейрона

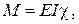
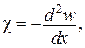
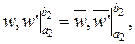
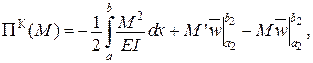
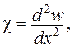
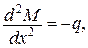
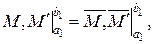
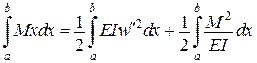
Відповідні екстремальні значення функціоналів Лагранжа і Кастільяно співпадають.

Варіаційні рівняння функціоналів Лагранжа і Кастільяно утворюють так звану пару двоїстих задач варіаційного числення, коли попередні умови однієї задачі є природними умовами іншої і навпаки. Під природними умовами розуміються умови, яким задовольняють відповідні варіаційні рівняння.

За допомогою методу множників Лагранжа можна “поміняти місцями” додаткові і природні умови, тобто із функціонала Лагранжа отримати функціонал Кастільяно і навпаки. Таке перетворення у варіаційному численні має назву перетворення Фрідріхса. Зазначимо, що екстремальні значення функціоналів Лагранжа і Кастільяно, а також усіх функціоналів, які отримані за допомогою множників Лагранжа співпадають.

Лекція 9