Інтегральні перетворення Лапласа та Меллліна.

Трансформанта перетворення Лапласа зображується у формі:

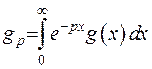(2.33)

Відновимо вихідну функцію 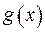, продовжуючи її нулем на від’ємній частині осі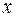

,

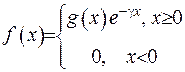де 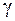- деяке довільне число.

Скористуємося формулою (2.29):

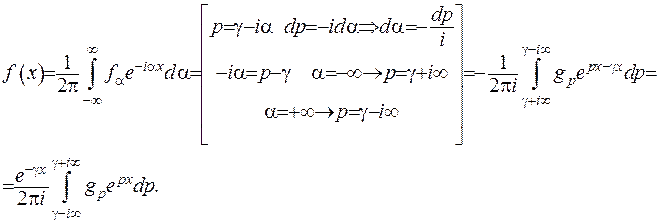
Якщо взяти тільки додатні значення 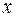, то отримуємо рівність:

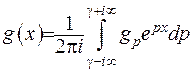. (2.34)

Ця формула є справедливою у випадку, коли вихідна функція 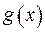задовольняє умовам

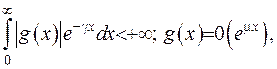
де .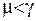

Формули (2.33), (2.34) є відповідно формулами прямого та оберненого інтегрального перетворення Лапласа.

Нехай трансформанта Мелліна функції 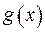має вигляд

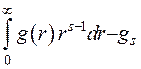. (2.35)

Відшукаємо вихідну функцію 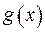. Для цього використаємо формулу перетворення Фур’є, де зробимо попередньо заміну змінних:

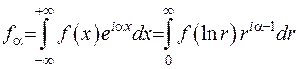, (2.36)

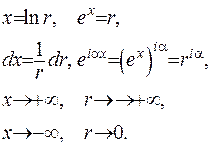
У отриманому інтегралі зробимо нові позначення, а саме: 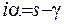, тоді 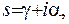де

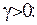
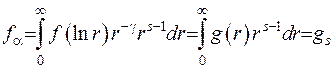, (2.37)

де 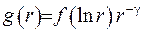. Для трансформанти Фур’є (2.37) використаємо формулу обернення, де зробимо також заміну змінних:

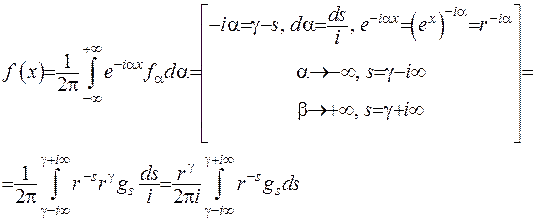(2.38)

Формула (2.38) є формулою оберненого перетворення Мелліна.

Зафіксуємо параметр 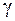та розглянемо інтеграл

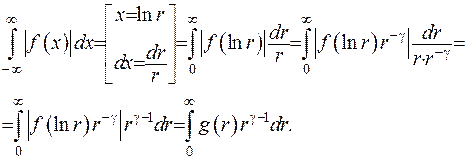
Оскількі інтеграл в лівій частині рівності є абсолютно збіжний, то і інтеграл в правій частині має бути збіжним. Отримано умову, при виконані якої є справедливою формула обернення (2.38). Щоб інтеграл збігався на 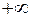, потрібно взяти 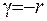, а для збіжності у точці 0 величина 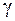має задовольняти умові 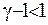, тобто .

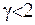Таким чином, ми познайомилися з методом інтегральних перетворень розв’язання задач математичної фізики, також розглянули властивості інтегральних перетворень Фур’є, Лапласа та Мелліна.

Наступний розділ містить матеріал, якій дозволяє ознайомиться з одним з найважливіших методів розв’язання одновимірних крайових задач – методом функції Гріна.