ІІІ.1. Побудова фундаментальної функції рівняння Лапласа. Ії фізичний сенс.
РІВНЯННЯ ЕЛІПТИЧНОГО ТИПУ З ЕЛЕМЕНТАМИ
ТЕОРІЇ ПОТЕНЦІАЛІВ.
Матеріал цього розділу присвячено дослідженню еліптичних рівнянь (найважливішим прикладом якого є рівняння Лапласа та Пуасона), а також особливо важливий з точки зору різних застосувань теорії потенціалу.
ІІІ.1. Побудова фундаментальної функції рівняння Лапласа. Ії фізичний сенс.
Нехай функція 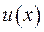 - функція багатьох змінних
- функція багатьох змінних 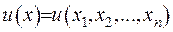 . Тут
. Тут 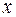 можна придати сенс вектора , а
можна придати сенс вектора , а 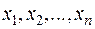 - його проекцій на вісі. Як відомо, відстань між двома довільними точками
- його проекцій на вісі. Як відомо, відстань між двома довільними точками 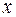 та
та  - вимірного простору вводиться за формулою
- вимірного простору вводиться за формулою
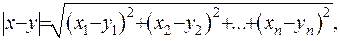
а для направляючих косинусів є вірною формула 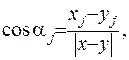
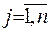 . Проілюструємо це наочно для просторового випадку
. Проілюструємо це наочно для просторового випадку 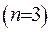 (див.рис.1).
(див.рис.1).
Розглянемо рівняння Лапласа
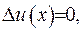 (ІІІ.1)
(ІІІ.1)
де 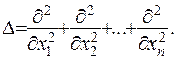
Покажемо, що функція
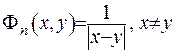 є
є
фундаментальним розв’язком
рівняння (ІІІ.1). Для цього підрахуємо
похідні 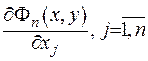 :
:
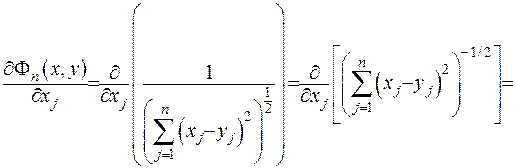
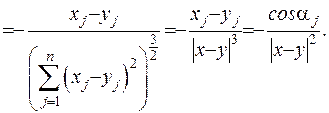
Підрахуємо тепер другу похідну:
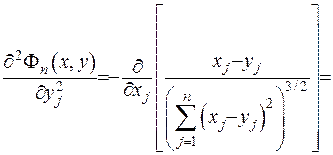
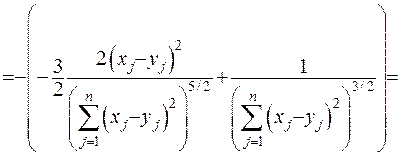
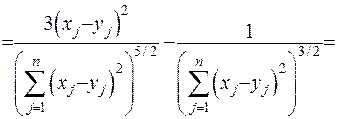
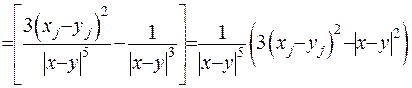 (ІІІ.2)
(ІІІ.2)
Зображення другої похідної (ІІІ.2) підставимо до рівняння Лапласа (ІІІ.1):
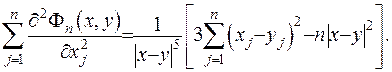 (ІІІ.3)
(ІІІ.3)
Якщо у формулі (ІІІ.3) взяти за 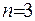 та врахувати, що
та врахувати, що 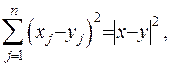 то рівняння Лапласа (ІІІ.1) буде задовільнено автоматично, що і означає, що функція
то рівняння Лапласа (ІІІ.1) буде задовільнено автоматично, що і означає, що функція 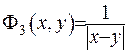 є його фундаментальним розв’язком.
є його фундаментальним розв’язком.
Аналогичним чином можна показати, що для випадку 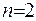 фундаментальний розв’язок потрібно брати у вигляді
фундаментальний розв’язок потрібно брати у вигляді 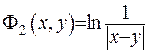 . Доведемо цей факт. Нехай
. Доведемо цей факт. Нехай 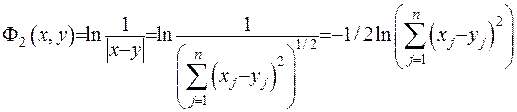
Знайдемо першу похідну функції:
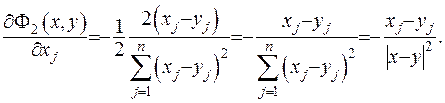
Для другої похідної функції отримаємо:
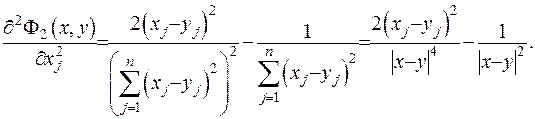
Одержані зображення для похідних підставимо до рівняння Лапласа (ІІІ.1), де візьмемо 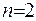 :
:
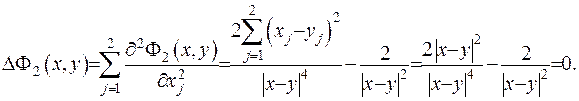
Встановимо фізичний сенс побудованого фундаментального розв’язку.
Використаємо закон всесвітнього тяжіння, який проілюструємо на прикладі. Нехай у просторі розташовано два тіла з масами 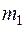 та
та 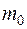 відповідно, що притягуються одне до одного з силою
відповідно, що притягуються одне до одного з силою 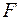 , абсолютна величина якої прямо пропорціональна масам цих тіл та обратно пропорціональна квадрату відстані між ними:
, абсолютна величина якої прямо пропорціональна масам цих тіл та обратно пропорціональна квадрату відстані між ними: 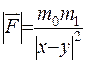 , де
, де 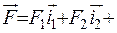
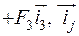 - направляючи орти,
- направляючи орти, 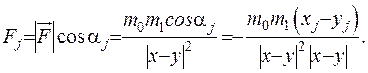
Якщо припустити, що 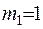 , то
, то 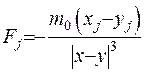 ,
, 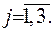
Введемо означення потенціалу силового поля. Функція 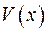 є потенціалом силового поля, якщо її градієнт зображує силу притяжіння одиничної маси до заданої:
є потенціалом силового поля, якщо її градієнт зображує силу притяжіння одиничної маси до заданої:
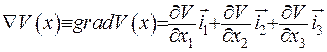 .
.
За цим означенням, як бачимо, фундаментальний розв’язок – це є потенціал силового поля, який визначає тяжіння одиничної маси, що зосереджена у точці  до одиничної маси, що зосереджена у точці
до одиничної маси, що зосереджена у точці  . Це і визначає фізичний сенс фундаментальної функції.
. Це і визначає фізичний сенс фундаментальної функції.
Наприклад, у випадку 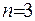 маємо:
маємо:
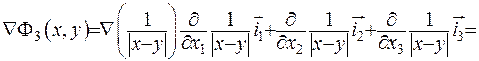
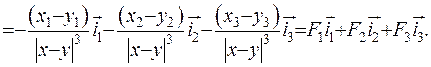
Розглянемо випадок, коли у точках 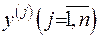 зосереджені маси
зосереджені маси 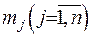 . Потенціал, який створюється цими масами та притягуючий одиничну масу, зосереджену у точці
. Потенціал, який створюється цими масами та притягуючий одиничну масу, зосереджену у точці 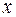 , описується за формулою:
, описується за формулою:
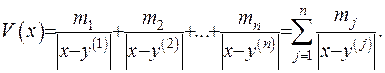
Дата добавления: 2016-05-05; просмотров: 818;
