Виведення рівняння теплопровідності.

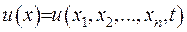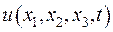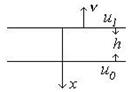
Позначимо температуру середовища у будь-який точці середовища, як ; у випадку тривимірного середовища це буде функція . Як відомо, температура завжди переходить з більш нагрітої у менш нагріту область простору. Нехай 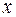- це тепловий потік, що тече з однієї частини шару товщини 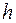в іншу у напрямку нормалі (див.рис.1). Будемо вважати, що один край має температуру 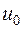, а інший -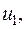 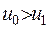. Розглянемо частину поверхні цього шару, де виділимо циліндр площиною 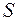, з’ясуємо, яка кількість тепла прямує через такий циліндр, об’єм якого дорівнює 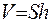. Позначимо цю шукану кількість тепла через 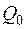. Зрозуміло, що величина 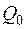є пропорційною до різниці температур та площі поверхні 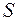та обратнопропорційною до товщини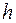

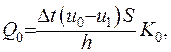(1.14)

де 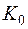- коефіцієнт теплопровідності, який встановлено експериментально, 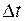- це проміжок часу, на протязі якого досліджується процес.

Приймемо, що кількість тепла 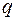, що за одиницю часу проходить через одиницю поверхні, визначається за формулою

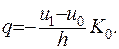(1.15)

Прямуючи 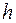до нуля, отримаємо

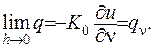(1.16)

Формула (1.15) описує тепловий потік через поверхню.

Встановлено, яку кількість тепла потрібно підвести до об’єма 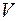з відомою масою 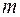для того, щоб його температура підвищилася на величину

:

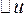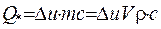, (1.17)

тут 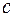є коефіцієнт теплоємкості, 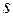- густина шару.

Знайдемо 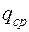- кількість тепла, яку потрібно подавати в одиницю часу до одиниці об’єма

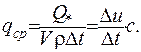
Зробивши перехід до межі при

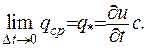(1.18)

Виділимо елементарний об’єм у просторі (див.рис.2)

Позначимо за - кількість тепла, що входить у паралелепіпед через 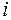- ту грань, тобто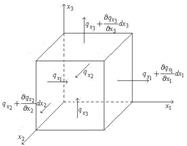

тепловій потік через 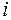- ту грань, а за -

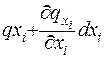Рис. 2 кількість тепла, що виділяється з паралелепіпеду

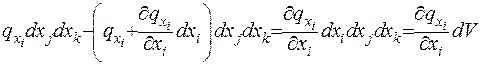(1.19)

Використовуючи формули (1.14) – (1.16), отримаємо

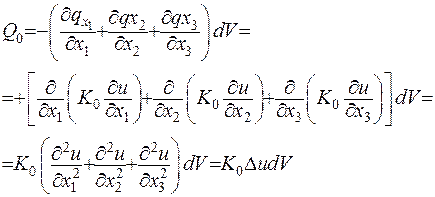(1.20)

Остаточно маємо

,

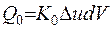де 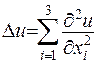- оператор Лапласа.

Формула (1.20) визначає кількість тепла, що залишилася у паралелепіпеді, коли через всі три його границі прямує тепловий потік.

Якщо у середині паралелепіпеда генерується тепло 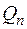, то загальна кількість тепла у паралелепіпеді обчислюється за формулою

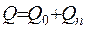, (1.21)

де 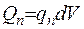, 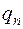- кількість тепла, що у одиницю часу проходить одиницю об’єму, коли усередині існує джерело тепла.

З іншого боку кількість тепла, яку потрібно подавати в одиницю часу до одиниці об’ема, визначається за формулою (1.18). Дорівнявши обидві частини рівностей, отримаємо:

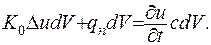(1.22)

Якщо ввести позначення 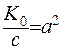та поділити обидві частини співвідношення (1.22) на 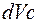, то рівняння набуває вигляду

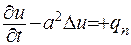. (1.23)

Рівняння виду (1.23) і є рівнянням теплопровідності.

У випадку, коли температура не змінюється за часом, то часткова похідна за часом дорівнює нулеві:

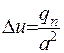(1.24)

Рівняння виду (1.24) називають рівнянням Пуассона.

Якщо джерел тепла усередині немає, то рівняння Пуассона стає однорідним:

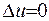(1.25)

Рівняння (1.25) називають рівнянням Лапласа (або гармонічним рівнянням)

Друге класичне рівняння математичної фізики це рівняння коливань струни.