Зведення задачі Штурма-Ліувилля до інтегрального рівняння. Необхідність розв’язання задачі Штурма-Ліувилля виникає кожного разу, коли необхідно звести диференціальне рівняння у часткових похідних до звичайного

Необхідність розв’язання задачі Штурма-Ліувилля виникає кожного разу, коли необхідно звести диференціальне рівняння у часткових похідних до звичайного диференціального рівняння

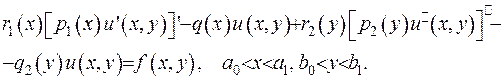(2.64) Під час застосування для цього методу інтегральних перетворень потрібно побудувати ядро перетворення, яке має задовольнити таку крайову задачу:

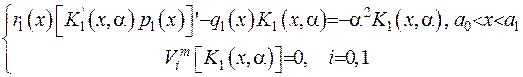(2.65)

Спростимо цю задачу Штурма-Ліувилля та зведемо її до стандартного вигляду. Позначимо 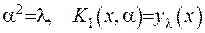та помножимо обидві частини рівняння з (2.65) на 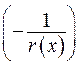. Надалі будемо вважати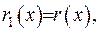

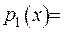
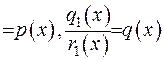. Тоді крайова задача (2.65) буде записуватися наступним чином:

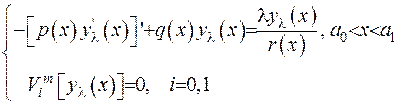(2.66)

Форма (2.66) є стандартною формою крайової задачі Штурма-Ліувилля.. Введемо оператор Штурма-Ліувилля

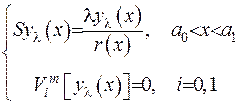(2.67)

де .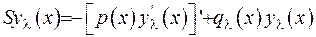

Існує два основних випадка задачі Штурма-Ліувилля (2.67):

1) регулярний випадок – якщо: а) інтервал, на якому змінюється змінна є скінченний; б) всі функції та їх похідні є неперервними на цьому інтервалі; в) функція .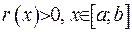

2) нерегулярній випадок – якщо порушена хоча б одна з умов а),б), в).

Розглянемо допоміжну крайову задачу та доведемо, що вона є самоспряженою:

(2.68)

Для цього спершу доведемо, що диференціальний оператор 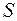є самоспряженим:

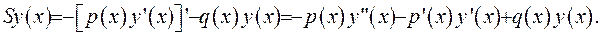
Якщо згадати загальний вигляд диференціального оператора другого порядку

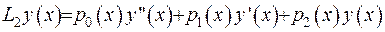, та спряжений до нього можна записати наступним чином:

Порівняємо оператор 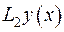з оператором Штурма-Ліувилля 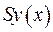. Як бачимо, .

Тепер порівняємо коефіцієнти оператора Штурма-Ліувилля с коефіцієнтами спряженого оператора. Коефіцієнти при старшій похідної збігаються. Порівняємо їх при першій похідній: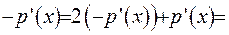

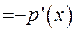. Далі проведемо порівняння при значеннях функції :

.

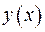Знайдемо умови, за виконанню яких оператор Штурма-Ліувилля є самоспряженим: 1) 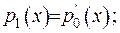2) .

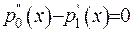Тепер залишається перевірити інтегральну умову. Нехай існує дві функції 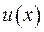та 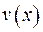, що задовольняють дві наступні піводнорідні крайові задачі

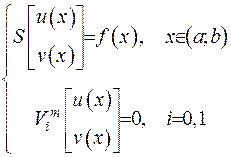
Доведемо, що виконується рівність . Дійсно, підставимо замість скороченого запису оператора Штурма-Ліувилля його повну форму:

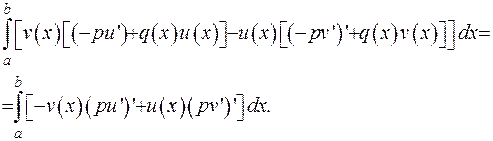
Отриманий інтеграл проінтегруємо за частинами:

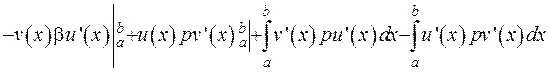. (2.69)

Для того, щоб підрахувати у виразі (2.69 ) підстановки, використаємо крайові функціонали:

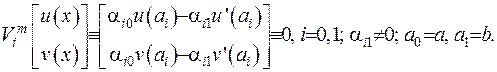
Звідки маємо, що Підставимо до виразу (2.69) отримані співвідношення:

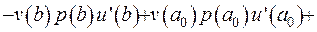
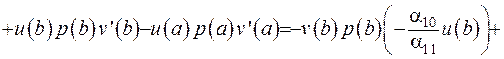
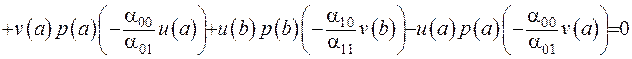Інтегральну умову виконано. Тим самим доведено, що крайова задача Штурма-Ліувилля є самоспряженою, отже її розв’язок можна записати за допомогою функції Гріна:

(2.70)