Теорема про існування функції Гріна. Перший спосіб побудови.

Теорема. Якщо крайові умови задачі є неособливими, то для такої задачі завжди існує функція Гріна.

Доведення. Проведемо доведення за конструктивним шляхом. Припустимо, що фундаментальна система розв’язків (ФСР) диференціального рівняння 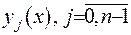є відомою. Побудуємо функцію двох змінних таким чином, щоб як більше властивостей функції Гріна було б виконано. Наприклад:

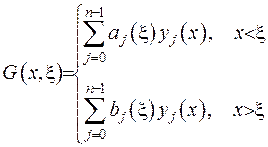(2.50)

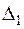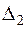Помітимо, що властивість 3) теореми для областей та виконано завдяки тому, що фундаментальні розв’язки мають неперервні похідні до 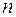-го порядку.

Будемо намагатися виконати залишившися властивості. З цією метою підрахуємо 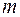-ту похідну функції:

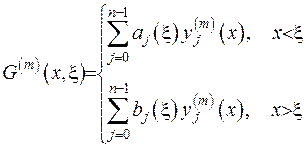
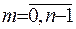
Для того, щоб виконувалась неперервність всіх похідних до 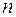-го порядку, вимагатимемо умову

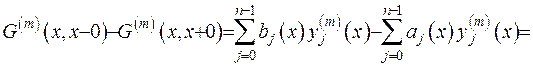
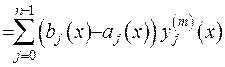при 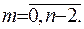(2.51)

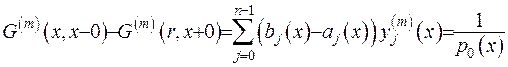(2.52)

при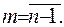

Рівності (2.51), (2.52) утворили неоднорідну систему 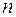рівнянь з 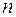невідомими коефіцієнтами 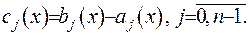Визначник отриманої системи відмінений від нуля 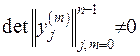за рахунок того, що 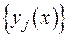є ФСР. Отже, система має єдиний розв’язок, тобто коефіцієнти 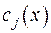відшукаємо єдиним чином. Першу та другу властивість теореми задоволено.

Для того, щоб виконувалась властивість 4), потрібно підібрати коефіцієнти. Підрахуємо похідні від функції 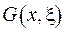за першою змінною на обох кінцях інтервалу :

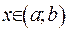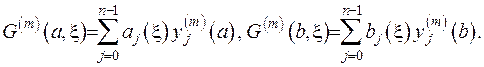
Знайдемо тепер 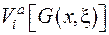та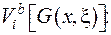

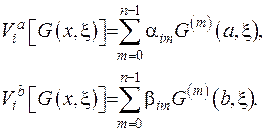
Зформуємо граничний функціонал:

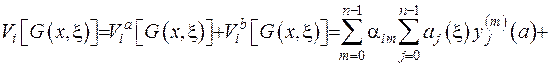
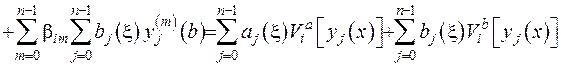(2.53)

Для виконання четвертої умови будемо вимагати, щоб граничний функціонал дорівнював нулеві:

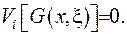
Додамо та віднімемо у правій частині співвідношення (2.53) вираз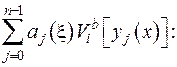

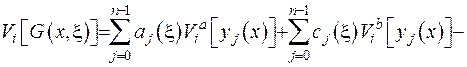
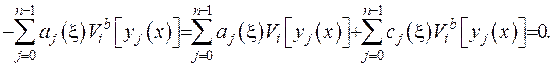(2.54)

Коефіцієнти 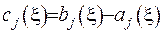було визначено раніше. Таким чином, отримано наступну рівність:

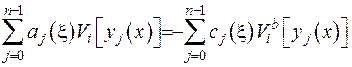(2.55)

Система (2.55) є системою лінійних алгебраічних рівнянь відносно невідомих коефіцієнтів 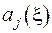. Визначник цієї системи відмінен від нуля 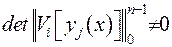. Це забезпечено тим, що крайові умови є неособливими. Отже, система є розв’язуємою і всі її коефіцієнти є визначені. Виконано всі чотири умови та закінчено побудову функції Гріна.