Визначення функції Гріна. Неособливі крайові умови задачі математичної фізики.

Розглянемо наступну одновимірну крайову задачу

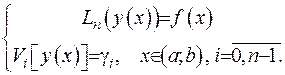(2.39)

Тут 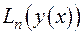- диференціальний оператор 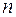-го порядку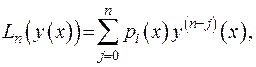

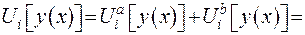
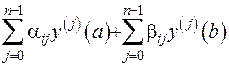. Вважається, що коефіцієнти 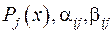- дійсні, зокрема .

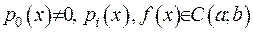Розв’яжемо одновимірну крайову задачу (2.39). Це означає, що потрібно розшукати розв’язки диференціального рівняння (2.39) та знайти з них той, що задовольняє крайові умови з (2.39). Як відомо з курсу диференціальних рівнянь, кількість розв’язків дорівнює порядку старшої похідної однорідного рівняння фундаментальної системи диференціального рівняння (2.39), а розв’язки мають задовольняти умову

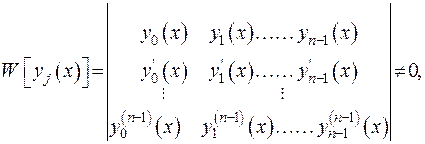(2.40)

де 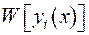- Вронскіан фундаментальної системи розв’язків (у наступному ФСР). Умова (2.40) забезпечує лінійну незалежність ФСР однорідного рівняння 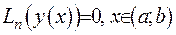. Граничні умови з (2.39) є неособливими. Неособливими будемо вважати умови, для яких виконується 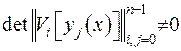. (У протилежному випадку умови будемо називати особливими.) Проведено також класифікацію одновимірних задач. Розглянемо три наступні одновимірні крайові задачі:

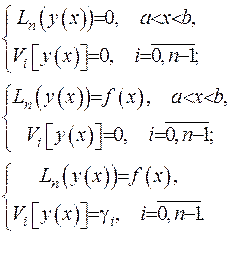(2.41)

Перша задача з (2.41) є однорідною одновимірною крайовою задачею, друга – півнеоднорідною одновимірною крайовою задачею, а третя – повністю неоднорідною. Спершу вивчемо одновимірні однорідні крайові задачі.

Теорема. Якщо граничні умови однорідної одновимірної крайової задачі є неособливими, то однорідна крайова задача має тільки тривіальний розв’язок.

Доведення.

Загальний розв’язок диференціального рівняння зобразимо у вигляді суперпозиції його ФСР: 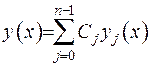. Задовольнимо крайові умови:

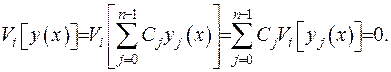
Таким чином, отримано систему лінійних алгебраїчних рівнянь відносно невідомих коефіцієнтів 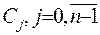. Визначник цієї системи відмінен від нуля, за рахунок властивості ФСР (2.40). Тобто всі коефіцієнти 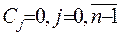. Отже, .

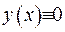Для півнеоднорідної одновимірної крайової задачі розглянемо функцію Гріна та її властивості. За допомогою цієї функції розв’язок рівняння відповідної задачі запишемо у вигляді:

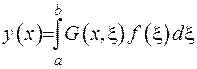. (2.42)

У випадку неоднорідної одновимірної крайової задачі для побудови розв’язку потрібно, окрім ФСР та функції Гріна, знайти ще базисну систему розв’язків (БСР) 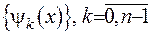, кожен член якої має задовольняти задачі

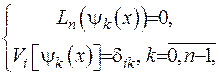(2.43)

де 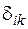- символ Кронекера.

Отримавши функцію Гріна та БСР, розв’язок неоднорідної задачі подаємо у зображенні

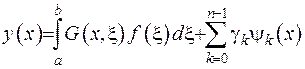. (2.44) Доведемо це.

Теорема. Зображення (2.44) є розв’язком неоднорідної одновимірної крайової задачі.

Доведення. Доведення буде складатися з двох частин. Спершу продемонструємо, що вираз (2.44) дійсно є розв’язком відповідного диференціального рівняння, для чого застосуємо до нього диференціальний оператор

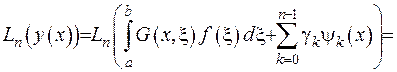
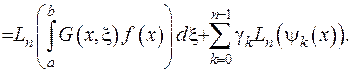(2.45)

Останній задаток у співвідношенні (2.45) дорівнює нулеві за рахунок ознаки БСР, а перший за рахунок формули (2.42) дорівнює .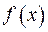

Таким чином, доведено, що функція (2.44) задовольняє диференціальне рівняння. Перевіримо тепер, що вона задовольняє граничні умови. З цією метою застосуємо до неї крайовий функціонал

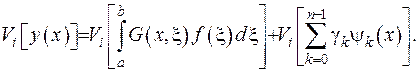
За рахунок того, що функція Гріна задовольняє півнеоднорідній крайовій задачі, перший доданок дорівнює нулеві. Другий доданок перепишемо у вигляді

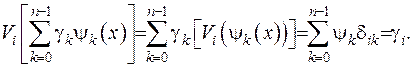
Отже, .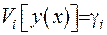

Довели, що зображення (2.44) є розв’язком неоднорідної одновимірної крайової задачі.

Як бачимо, принципово важливим у побудові розв’язку є наявність функції Гріна. Розглянемо її основні властивості.