IV.1. Постановка початково-крайової задачі.

РІВНЯННЯ ПАРАБОЛІЧНОГО ТИПУ.

Фізичні явища, пов’язані з процесами теплопровідності та дифузії, з розповсюдженням електромагнітних полів, з рухом в’язкої рідини, описується рівнянням параболічного типу. Найпростішим їх прикладом є рівняння теплопровідності.

IV.1. Постановка початково-крайової задачі.

Типовим представником цього класу рівнянь є рівняння нестаціонарної теплопровідності.

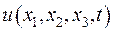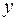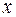Будемо позначати через температуру точці трьохвимірного простору 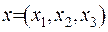в момент часу 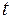. Ця функція задовольняє рівняння

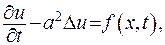(IV.1)

де 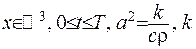- коефіцієнт теплопровідності, 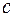- коефіцієнт теплоємкісті, 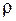- густина, 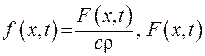- потужність джерел тепла, 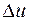- оператор Лапласа - .

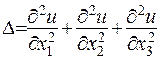Рівняння (IV.1) є рівнянням параболічного типу та має нескінченну множину розв’язків. З метою відокремлення єдиного розв’язка потрібно задати крайові умови та початкові умови. Доведемо, що якщо такі умови задано, то задача буде мати не більше одного розв’язка.

Постановка початково-крайової задачі.

Потрібно відшукати функцію 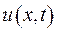, яка задовольняє диференціальне рівняння

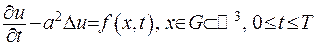(IV.2)

та крайові умови

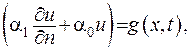(IV.3)

де 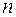- нормаль до поверхні 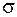, що обмежує область 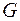, 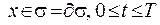. Також мають виконуватися початкові умови

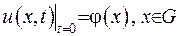. (IV.4)

Примітка: якщо у рівняння (IV.2) 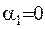, то отримаємо першу крайову задачу; якщо 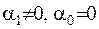, то отримаємо другу крайову задачу; якщо 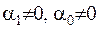, то отримаємо загальний випадок – третю крайову задачу.