IV.2. Принцип максимуму.

Розглянемо випадок, коли 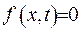та припустимо, що 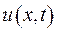неперервна при 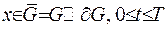. Будемо вважати, що функція 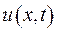сягає свого максимуму або у деякий точці 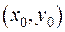, тобто 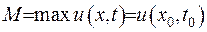, , 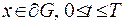або вона сягає свого максимуму у початковій момент часу: 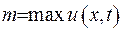, 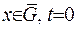. Взагалі кажучи, має місце нерівність .

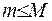Теорема.

Якщо виконуються наступні умови, а саме:

1) 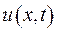- неперервна функція при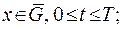

2) виконується однорідне рівняння теплопровідності:

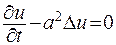при

3) функція 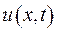сягає свого максимуму у точці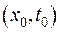

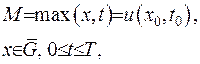
то ця точка або лежить на границі нагрітого тіла, або цього максимуму функція сягає в початковий момент часу:

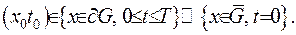
Доведення.

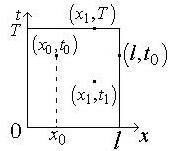
Розглянемо одновимірний випадок: . Доведення проводитиметься від протилежного, а саме – припустимо, що точка 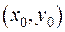лежить усередині області: 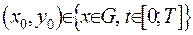. Доведемо, що тоді існує точка 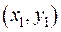, де порушено рівняння (IV.1).

Розглянемо функцію

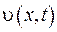
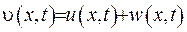, (IV.5)

де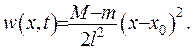

Знайдемо її максимум:

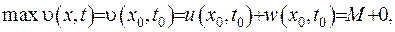
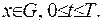(IV.6)

З іншого боку:

якщо , (IV.7)

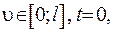або або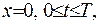

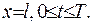
У (IV.7) враховано, що 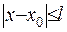. З нерівностей (IV.6) та (IV.7) випливає наступне: функція 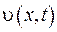сягає свого максимуму усередині області 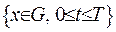. Позначимо цю точку 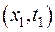. Тоді по означенно максимуму маємо,що 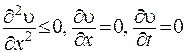,звідки: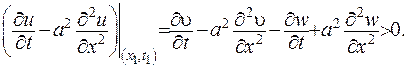

Отримано, що рівняння (1) порушено у точці 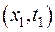. Теорему доведено.

З принципу максимуму легко отримати такі ствердження:

1)Розв’язок рівняння 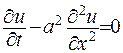сягає свого мінімального значення в початковий момент часу або на границі області.

Доведення базується на той самій схемі, що і доведення принципу максимуму для функції .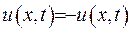

2)Функція 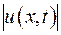сягає свого максимального значення в початковий момент часу або на границі області.