IV.3. Теореми єдності та стійкості розв’язка початково-крайової задачі.
Теорема єдності.
Початкова-крайова задача
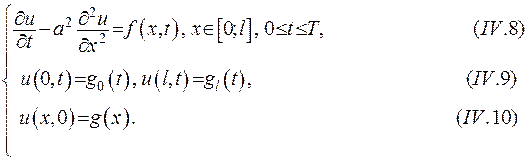
має не більше ніж один розв’язок.
Доведення.
Припустимо, що 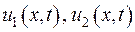 є розв’язками задачі (IV.8) – (IV.10). Введемо нову функцію
є розв’язками задачі (IV.8) – (IV.10). Введемо нову функцію 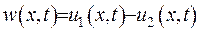 . Як бачимо, функція
. Як бачимо, функція 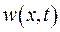 задовольняє рівняння (IV.8). Також для неї виконуються крайові умови
задовольняє рівняння (IV.8). Також для неї виконуються крайові умови 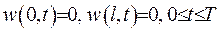 та початкова умова
та початкова умова 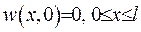 . З принципу максимуму випливає, що
. З принципу максимуму випливає, що 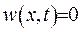 . А звідки і те, що
. А звідки і те, що 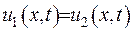 .
.
Теорема стійкості.
Малим змінам заданих функцій у початково-крайовій задачі
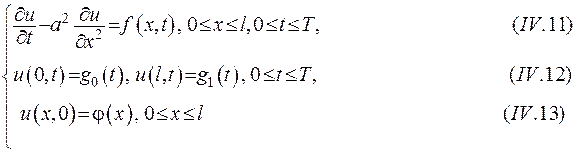
відповідають мали зміни розшукуємого розв’язку.
Доведення.
Розглянемо задачу з похибкою у початкових та крайових умовах:
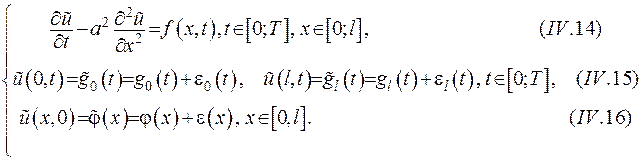 За
За 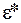 візьмемо
візьмемо 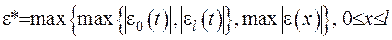 - максимальну похибку в умовах (IV.15), (IV.16). Покажемо, що для будь-яких
- максимальну похибку в умовах (IV.15), (IV.16). Покажемо, що для будь-яких 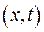 похибка у розв’язку не перевищує похибки у крайових та початкових умовах:
похибка у розв’язку не перевищує похибки у крайових та початкових умовах: 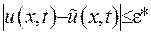 .
.
Побудуємо функцію 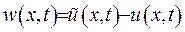 . Вона є розв’язком відповідної початково-крайової задачі:
. Вона є розв’язком відповідної початково-крайової задачі:
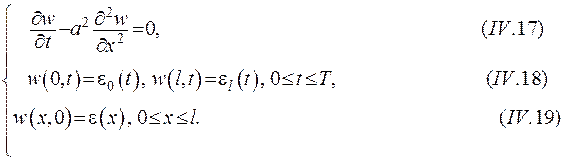
Відповідно до принципу максимуму для будь-якої точки 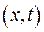 виконується
виконується
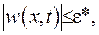
що і потрібно було довести.
IV.4. Задача Коші.
Постановка задачі.
Під час дослідження процесу теплопровідності у точках, що розташовані на досить великій відстані від границі тіла, впливом граничних умов можна нехтувати та вважати тіло нескінченним. У такій постановці виникає задача Коші – потрібно відшукати розв’язок рівняння теплопровідності при заданих початкових умовах
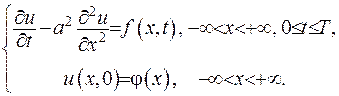 (IV.20)
(IV.20)
(IV.21)
У більшості випадків до задачі Коші додається умова або обмеженості розв’язку 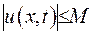 , або прямування його до нуля на нескінченності
, або прямування його до нуля на нескінченності 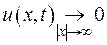 .
.
Єдність розв’язку.
Теорема.
Задача Коші (IV.20), (IV.21) має не більш ніж один обмежений розв’язок.
Доведення. Проводитиметься від протилежного. Нехай існує два різних обмежених розв’язка задачі Коші 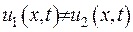 . Побудуємо нову функцію
. Побудуємо нову функцію 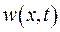 за формулою
за формулою 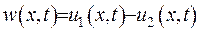 , відносно якої запишемо задачу Коші:
, відносно якої запишемо задачу Коші:
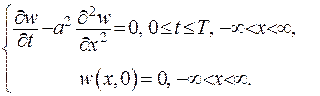 (IV.22)
(IV.22)
(IV.23)
З умови обмеженості розв’язків 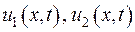 випливає обмеженість функції
випливає обмеженість функції 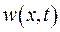 :
:
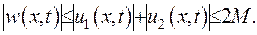 (IV.24)
(IV.24)
для будь-яких 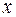 та
та 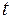 .
.
Введемо ще одну допоміжну функцію наступного вигляду:
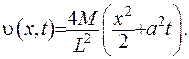 (IV.25)
(IV.25)
Легко переконатися, що зображення (IV.25) є розв’язком рівняння теплопровідності. Зафіксуємо будь-яке значення 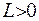 , та порівняємо обидві функції
, та порівняємо обидві функції 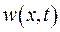 та
та 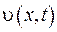 у області
у області 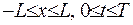 . Якщо
. Якщо 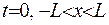 , то
, то 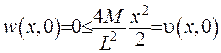 .Якщо
.Якщо 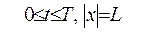 ,то
,то 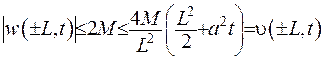 .
.
Враховуючи отримані оцінки та користуючись принципом максимуму, довели, що для будь-якого 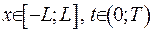 виконано нерівності
виконано нерівності 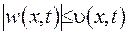 .
.
Зафіксуємо точку 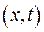 та спрямуємо
та спрямуємо 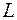 до нескінченності. Отримаємо, що
до нескінченності. Отримаємо, що 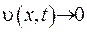 .
.
Функція 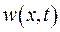 від величини
від величини 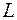 не залежить, звідки маємо, що
не залежить, звідки маємо, що 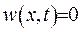 . Отже, розв’язки
. Отже, розв’язки  та
та 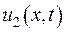 співпадають.
співпадають.
Дата добавления: 2016-05-05; просмотров: 1218;
