IV.5. Побудова фундаментального розв’язку рівняння теплопровідності.

Фундаментальний розв’язок однорідного рівняння теплопровідності , де зображується за формулою

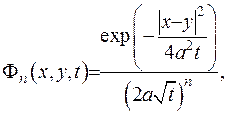(IV.26)

де відстань між точками введена як .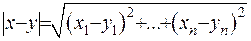

Доведемо цей факт. З цією метою покажемо, що функція (IV.26) задовольняє рівняння теплопровідності, а для цього підрахуємо відповідні похідні:

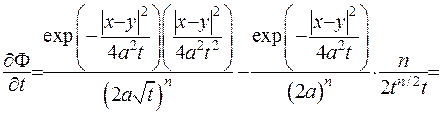(IV.27)

,

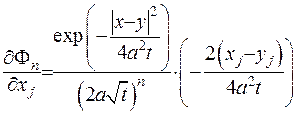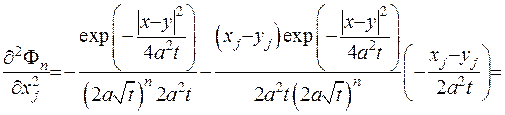
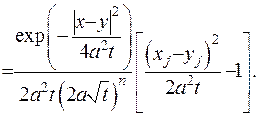(IV.28)

Підставимо співвідношення (IV.27), (IV.28) до рівняння теплопровідності:

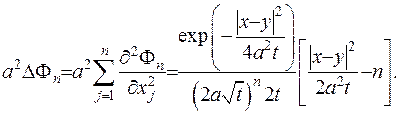(IV.29)

Як бачимо, порівнявши вирази (IV.29) та (IV.27), обидві частини рівняння співпадають. Доведено, що функція (IV.26) є фундаментальним розв’язком рівняння теплопровідності.

Dведемо для скорочення запису диференціальний оператор 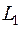: 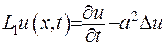- оператор теплопровідності. Доведено, що 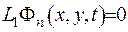. Покажемо, як зображується розв’язок задачі Коші через фундаментальну функцію:

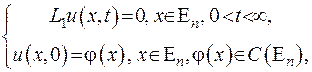(IV.30)

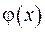- неперервна та обмежена функція.

Доведемо, що розв’язок задачі Коші (IV.30) має вигляд:

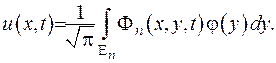(IV.31)

Розглянемо випадок - одновимірну задачу.

(IV.32)

Щоби довести, що 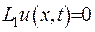, потрібно внести диференціальний оператор під знак інтеграла: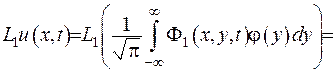

. Але для цього маємо попередньо довести, що вихідний невласний інтеграл (IV.32) є рівномірно збіжним за обома змінними, - це по-перше. По-друге – маємо показати, що після внесення оператора він також залишається рівномірно збіжним.

З цією метою зробимо заміну змінних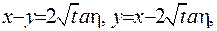

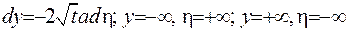. У новій змінній інтеграл (IV.32) прийме вигляд:

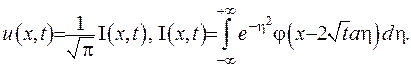(IV.33)

Покажемо рівномірну збіжність відносно параметрів та невласного інтеграла (IV.33). Промажоруємо цей інтеграл інтегралом, який буде у свою чергу збіжним та не буде залежати від цих параметрів:

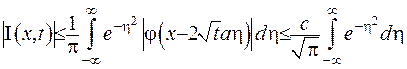(IV.34)

Інтеграл, що отримано у нерівності (IV.34), є збіжним, звідки за критерієм Вейєрштраса випливає, що інтеграл (IV.32) є рівномірно збіжним за змінними та .

Внесемо оператор 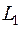під знак інтегралу та доведемо його збіжність:

.

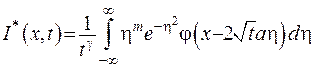Підберемо для цього інтегралу мажоруючий. Якщо взяти за максимальне значення , то отримаємо

.

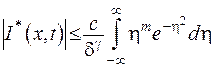Інтеграл тут є незалежним від змінних та , та є збіжним. Отже, доведено, що вихідний інтеграл є рівномірно збіжним за змінними та , та після застосування оператора диференціювання він також є рівномірно збіжний.

Покажемо, що початкові умови також задоволено. Використаємо той факт, що 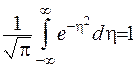, звідки маємо 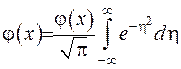. Розглянемо різницю:

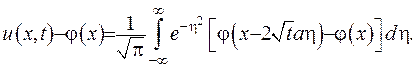(IV.35)

Розіб’ємо інтервал інтегрування у (IV.35) на 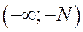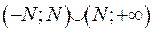, де 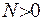. Отже, різниця функцій (IV.35) запишеться за формулою:

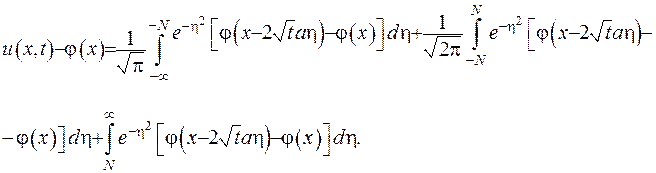(IV.36)

Покажемо, що різниця функцій (IV.36) прямує до нуля, коли прямує до нуля. Проведемо оцінку

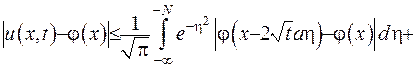(IV.37)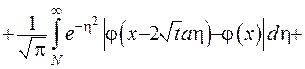

Враховуємо той факт, що функція 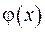є всюди неперервною в просторі 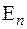, а значит є обмеженою, тобто

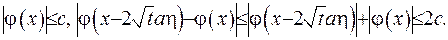
Отже, маємо

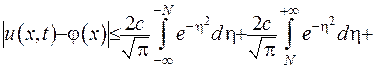
Інтеграл є збіжним, звідки випливає

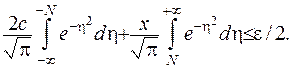(IV.38)

У залишившемуся інтегралі враховуємо те, що 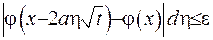, а інтеграл . Остаточно маємо

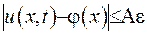при ,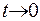

або іншими словами

(IV.39)

З співвідношення (IV.39) випливає, що початкові умови задовольнено.

Отже, розв’язок задачі Коші має вигляд (IV.31).