Зведення задачі Штурма-Ліувилля до інтегрального рівняння.

Нехай маємо наступну крайову задачу:

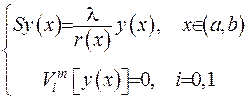(2.71)

Тут 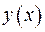- є власні функції задачі Штурма-Ліувилля. З доведеною вище формули (2.70 ) випливає, що розв’язок задачі (2.71) можна зобразити у формі:

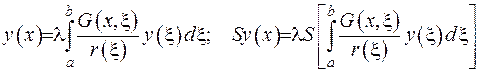(2.72)

Тобто показано, що розв’язати задачу Штурма-Ліувилля є еквівалентним до розв’язання рівняння (2.72). Тепер потрібно довести зворотне: розв’язання рівняння (2.72) еквівалентно розв’язанню відповідної задачі Штурма-Ліувилля - будь-який розв’язок рівняння (2.72) є розв’язком крайової задачі Штурма-Ліувилля. Застосуємо до рівняння (2.72) диференціальний оператор, тобто отримано праву частину рівняння, а з цього випливає, що диференціальне рівняння задачі задоволено. Перевіримо, що виконуються граничні умови. Це має місце за рахунок того, що функція Гріна побудовано таким чином, що граничні умови мають бути задоволені. Отже, показано, що розв’язок рівняння (2.72) є розв’язком задачі Штурма-Ліувилля. Доведемо повну еквівалентність задачі Штурма-Ліувилля та інтегрального рівняння.

Покажемо, що нетривіальний розв’язок задачі виникає лише для певних значень параметра 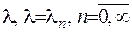, яких є лічильна множина. З цією метою приведемо інтегральне рівняння (2.72) до стандартного вигляду, для чого помножимо обидві частини на 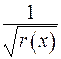та введемо позначення 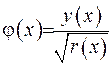. Рівняння (2.72) набуває вигляду:

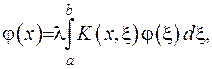(2.73)

де 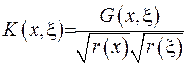. Або у інший формі можна записати:

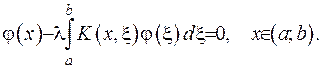(2.74)

Це є однорідне інтегральне рівняння Фредгольна з симетричним ядром (останнє випливає з властивості функції Гріна самоспряженої задачі). З властивостей інтегрального рівняння (2.74) випливає:

1) інтегральне рівняння з симетричним ядром, має лічильну множину власних чисел 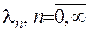. Розв’язки, що їм відповідають, - власні функції 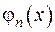задовольняють рівняння

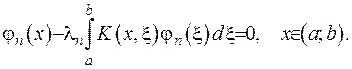
2) Власні функції, що відповідають різним власним значенням є ортогональними:

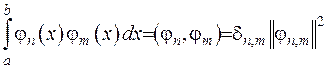(2.75)

Їх можна пронормувати. Якщо власні функції задачі Штурма-Ліувилля позначено 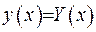та враховуючи, що власні функції інтегрального рівняння дорівнюють

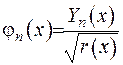, (2.76)

отримаємо умову ортогональності власних функцій Штурма-Ліувилля. З цією метою підставимо вираз (2.76) до співвідношення (2.75):

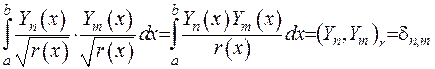(2.77)

Доведена ортогональність власних функцій задачі Штурма-Ліувилля з вагою .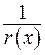

3) Доведемо тепер третю властивість власних функцій задачі Штурма-Ліувилля, що носить назву теореми розвинення Стеклова.

Теорема Стеклова.

Теорема. Будь-яку функцію 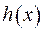, двічі неперервно диференцюєму на інтервалі 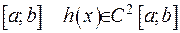та задовольняючу крайовим умовам Штурма-Ліувилля 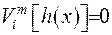, можна розвинути у рівномірно збіжний ряд за власними функціями задачі Штурма-Ліувилля.

Доведення. Нагадаємо теорему Гільберта-Шмідта з теорії інтегральних рівнянь, яка стверджує, що, якщо функцію 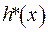зображено у вигляді

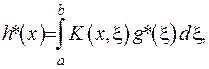(2.78)

то функцію 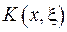може бути розвинено у равномірно-збіжний ряд за власними функціями інтегрального рівняння (2.78):

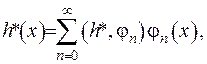(2.79)

де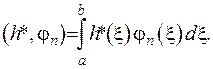

Використаємо цю теорему надалі під час доведення теореми Стеклова.

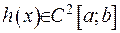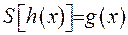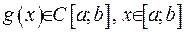Якщо за умовою теореми функція , то до неї можна застосувати оператор Штурма-Ліувилля: , де . Згідно умовам теореми, маємо 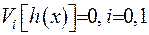. Для отриманої крайової задачі вже раніше побудовано функцію Гріна 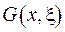. Отже, маємо записати розв’язок у вигляді:

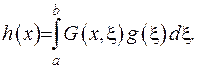
Домножимо обидві частини рівності на 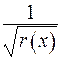та під знаком інтеграла помножимо та поділимо на 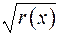. Введемо нові позначення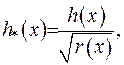

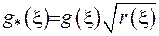. Отримано інтегральне рівняння:

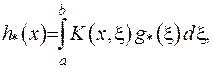
тут 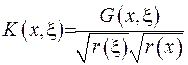. За теоремою Гільберта-Шмідта можемо зобразити функцію 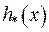у формі:

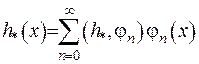
Запишемо скалярний добуток через власні функції задачі Штурма-Ліувилля:

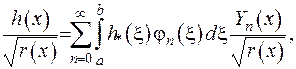(2.80)

або 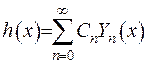, де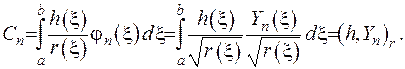

Отже, теорему Стеклова доведено.

Виведення формули обернення для інтегрального

перетворення на скінченому проміжку.

Нехай маємо диференціальне рівняння вигляду (2.64), до якого застосовано інтегральне перетворення за змінною 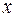з ядром перетворення :

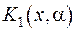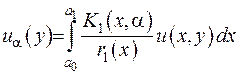
Як показано вище, ядро цього перетворення має задовольняти крайову задачу Штурма-Ліувилля і є її власною функцією 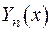, яка відповідає певному власному значенню :

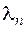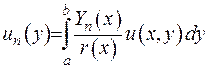(2.81)

На формулу (2.81) можна дивитися, як на зображення трансформанти інтегрального перетворення. Вихідна функція 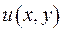має двічі неперервні похідні 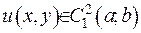та задовольняє граничні умови Штурма-Ліувилля 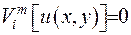. Згідно до теореми Стеклова її можна розвинути у ряд за системою власних функцій 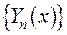відповідної задачі Штурма-Ліувилля:

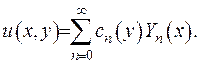(2.82)

Знайдемо зображення коефіцієнтів розвинення (2.82). З цією метою помножимо обидві частини рівності (2.82) на множник 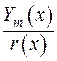та проінтегруємо на проміжку :

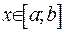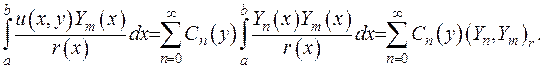(2.83)

Скалярний добуток, що входить у вираз (2.83), дорівнюватиме:

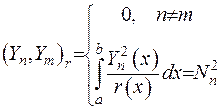
У випадку 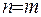маємо 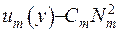, звідки випливає, що 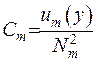. Підставивши отримане співвідношення до розвинення (40), здобудемо обернену формулу інтегрального перетворення на скінченому проміжку 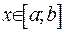, з прямим перетворенням (39):

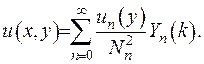(2.84)

Таким чином, ми познайомилися з таким важливим поняттям як функція Гріна одновимірних крайових задач та розглянули два різних метода її побудови.

Отже зараз, познайомимось з найважливішими методами розв’язання задач, більш детально та ретельно дослідимо властивості рівнянь основних типів математичної фізики.