Теорема про єдність існування функції Гріна.

Теорема. Якщо одновимірна крайова задача має неособливі крайові умови, то функція Гріна такої задачі є єдиною.

Доведення. Проводитиметься від протилежного. Припустимо, що існує дві різних функції Гріна 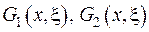таких, що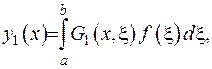

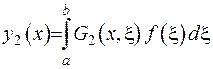- є розв’язками крайової задачі. Побудуємо функцію 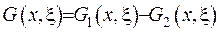. За рахунок того,що 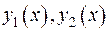є розв’язки рівнянь, запишемо 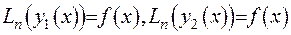. Побудуємо ще одну функцію 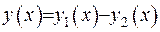та застосуємо до неї диференціальний оператор

.

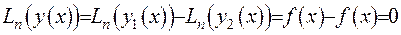З іншого боку,

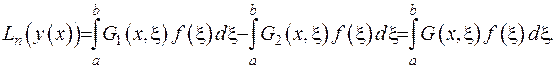
Отримали, що 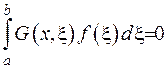для будь-якої правої частини рівняння 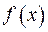. У зв’язку с тим, що функція є довільною, виберемо її у формі 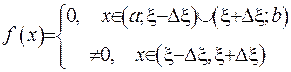. Розв’язок задачі у такому випадку, застосувавши теорему про середнє, запишемо у вигляді

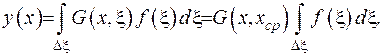
Згадаємо, що функція 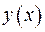є розв’язком однорідної крайової задачі, тобто має дорівнювати нулеві. Оскільки інтеграл в правій частині відмінений від нуля, то випливає, що 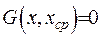. Функцію 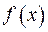вибрано довільним чином, тобто можемо зробити висновок, що 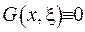. Звідки випливає, що 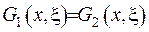. Єдність існування функції Гріна доведено.

З метою з’ясувати умови існування функції Гріна доведемо теорему про чотири визначальні властивості функції Гріна.