Теорема про чотири визначальні властивості функції Гріна.
Теорема. Якщо функція 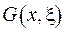 , що задана у прямокутнику
, що задана у прямокутнику 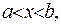
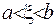 , має чотири наступні властивості, то ця функція є функцією Гріна півнеоднорідної крайової задачі:
, має чотири наступні властивості, то ця функція є функцією Гріна півнеоднорідної крайової задачі:
1) Функція Гріна та її похідні до 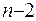 порядку
порядку 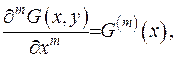
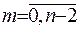 с неперервними у всій області;
с неперервними у всій області;
2) Похідна функції Гріна 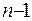 -го порядку є розривною на лінії
-го порядку є розривною на лінії 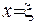 , та її стрибок дорівнює оберненому значенню коефіцієнта при старшій похідній
, та її стрибок дорівнює оберненому значенню коефіцієнта при старшій похідній 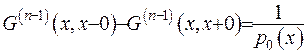 ;
;
3) Будь-яка похідна за змінною 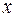 від функції Гріна є неперервною у областях
від функції Гріна є неперервною у областях 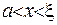 та
та 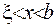 . У кожному з цих трикутників виконуватиметься рівняння
. У кожному з цих трикутників виконуватиметься рівняння 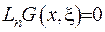 .
.
4) Функція Гріна має задовольняти граничні умови
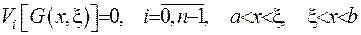 .
.
Доведення.
Розглянемо рис.4, та введемо позначення для областей 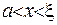 та
та 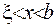 -
- 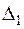
та 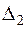 відповідно. Зобразимо розв’язок півнеоднорідної задачі (2.41), який має задовольняти функція Гріна, у вигляді
відповідно. Зобразимо розв’язок півнеоднорідної задачі (2.41), який має задовольняти функція Гріна, у вигляді
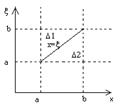
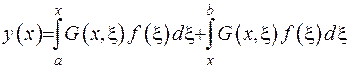 (2.46)
(2.46)
|
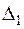 та
та 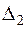 функція Гріна та її похідна є неперервними, тому при диференціюванні доданків у правій частині рівності (2.46) можна вносити похідну під знак інтеграла, враховуючи відомі формули:
функція Гріна та її похідна є неперервними, тому при диференціюванні доданків у правій частині рівності (2.46) можна вносити похідну під знак інтеграла, враховуючи відомі формули: 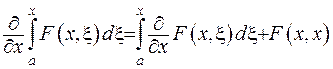 та
та 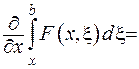
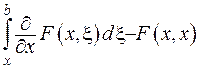 . З огляду на це, підрахуємо першу похідну:
. З огляду на це, підрахуємо першу похідну:
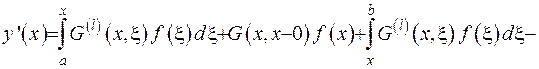
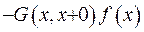 .
.
Спростимо отриманий вираз:
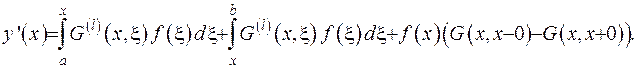 (2.47)
(2.47)
З умови неперервності функції Гріна останній доданок у рівності (2.47) дорівнює нулеві. За аналогічною схемою підрахуємо похідні функції Гріна до 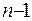 порядку
порядку
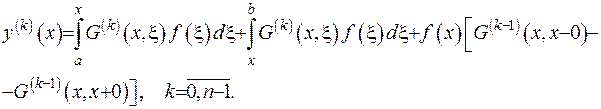
Останні доданки у всіх виразах дорівнювали нулеві за рахунок неперервності функції Гріна та її похідних за властивістю теореми. У випадку похідної 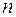 -го порядку матимемо
-го порядку матимемо
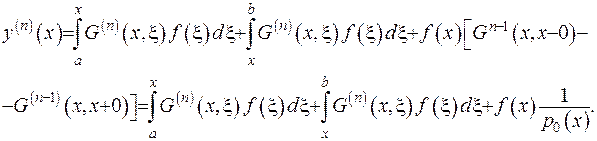
Остання рівність отримана за властивістю 2) теореми.
Підставимо тепер всі підраховані похідні у диференціальне рівняння
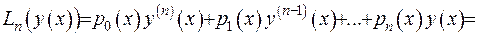
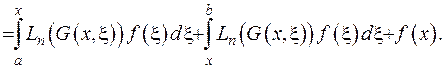
За рахунок властивості 3) теореми перші два доданка дорівнюють нулеві. Отже, отримано 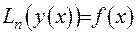 , тобто
, тобто 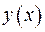 є розв’язком диференціального рівняння задачі. Покажемо, що функція
є розв’язком диференціального рівняння задачі. Покажемо, що функція 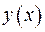 задовольняє крайові умови. З цією метою запишемо граничний функціонал у вигляді
задовольняє крайові умови. З цією метою запишемо граничний функціонал у вигляді
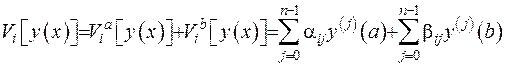 . (2.48)
. (2.48)
Підрахуємо похідні, що входять до граничних умов
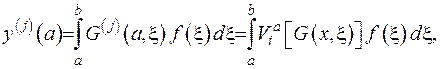
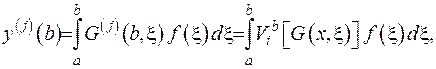
та підставимо ці співвідношення у рівність (2.48):
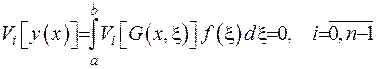 . (2.49)
. (2.49)
Рівність (2.49) отримано за рахунок властивості 4) теореми.
Доведено, що функція, яка задовольняє умовам 1) – 4) є функцією Гріна.
Слідство. Якщо з чотирьох умов теореми виконано тільки три перші умови, то функція 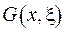 буде фундаментальною функцією:
буде фундаментальною функцією:
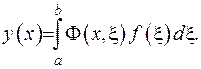
Дата добавления: 2016-05-05; просмотров: 855;
