А) Аксіома Лобачевського. Означення і властивості паралельних і розбіжних прямих в геометрії Лобачевського.
Аксіоматика геометрії Лобачевського складається з аксіом абсолютної геометрії та аксіоми Лобачевського
Аксіома Лобачевського.Існують принаймні одна пряма 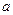 і одна точка
і одна точка 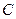 поза нею такі, що в площині, яку вони визначають, через точку
поза нею такі, що в площині, яку вони визначають, через точку 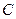 проходить принаймні дві прямі, що не перетинають пряму
проходить принаймні дві прямі, що не перетинають пряму 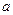 .
.
Аксіоматичні теорії евклідової геометрії та геометрії Лобачевського мають спільну частину – абсолютну геометрію.
Теорема. Через будь-яку точку, яка не належить довільній даній прямій, проходить принаймні дві прямі, що не перетинають дану пряму.
Теорема. Через точку, яка не належить даній прямій можна провести безліч прямих, що не перетинають дану пряму.
Далі будемо вважати всі прямі напрямленими. Тобто якщо використано символ  для прямої, то це означає, що на ній точка
для прямої, то це означає, що на ній точка  передує точці
передує точці  . При цьому будемо вважати, що всі необхідні нам точки прямої
. При цьому будемо вважати, що всі необхідні нам точки прямої 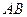 лежать між точками
лежать між точками 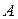 та
та 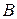 . Прямі
. Прямі 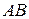 та
та 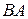 різні, або, інакше, два різні напрями на прямій, що проходить через точки
різні, або, інакше, два різні напрями на прямій, що проходить через точки 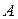 та
та 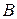 , визначаються різними порядками
, визначаються різними порядками 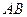 та
та 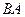 цих точок.
цих точок.
Означення. Пряма 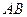 називається паралельною прямій
називається паралельною прямій 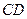 , якщо:
, якщо:
1) ці прямі не перетинаються;
2) для будь-яких точок 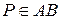 і
і 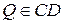 кожен внутрішній промінь кута
кожен внутрішній промінь кута 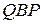 перетинає промінь
перетинає промінь 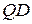 . Позначають
. Позначають 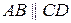 .
.
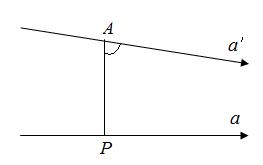
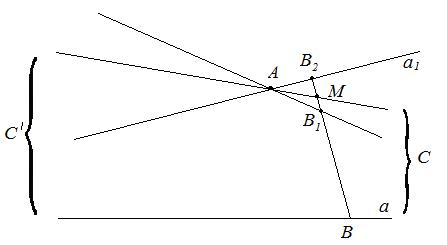
Теорема (ознака паралельності). Якщо прямі 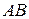 та
та 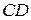 не мають спільних точок і існують такі точки
не мають спільних точок і існують такі точки 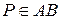 і
і 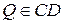 , що кожен внутрішній промінь кута
, що кожен внутрішній промінь кута 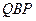 перетинає промінь
перетинає промінь 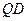 , то
, то 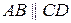 .
.
Теорема (існування паралельних прямих). Нехай дано пряму 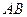 і точку
і точку 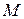 , яка не лежить на ній. Тоді в площині, яку вони визначають, існує і лише одна пряма
, яка не лежить на ній. Тоді в площині, яку вони визначають, існує і лише одна пряма 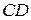 , яка проходить через точку
, яка проходить через точку 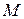 і паралельна прямій
і паралельна прямій 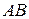 .
.
Наслідок.Нехай 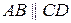 ,
, 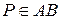 ,
, 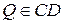 і
і 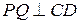 . Нехай також пари точок
. Нехай також пари точок 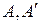 та
та 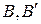 симетричні в осьовій симетрії відносно прямої
симетричні в осьовій симетрії відносно прямої 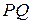 . Тоді пряма
. Тоді пряма 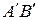 , яка буде симетричною прямій
, яка буде симетричною прямій 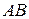 , паралельна прямій
, паралельна прямій 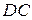 .
.
Остання теорема і наслідок з неї дають можливість сформулювати наступну теорему.
Теорема.Через точку, яка не належить заданій прямій, в даному на цій прямій напрямку можна провести тільки одну пряму, паралельну заданій. Через точку, яка не належить заданій прямій, можна провести дві прямі, паралельні заданій, але в різних напрямках.
Властивості відношення паралельності прямих:
1) (симетричність) якщо 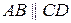 , то і
, то і 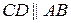 .
.
2) (транзитивність) якщо 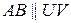 і
і 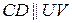 , то
, то 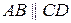 .
.
Означення.Нехай 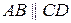 ,
, 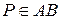 ,
, 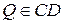 і
і 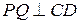 . Кут
. Кут 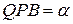 називається кутом паралельності, що відповідає відрізку
називається кутом паралельності, що відповідає відрізку 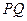 , який називають відрізком паралельності (або стрілкою).
, який називають відрізком паралельності (або стрілкою).
Теорема.Будь-який гострий кут може бути кутом паралельності. Або, інакше, яким би не був гострий кут, існує єдина пряма, яка перпендикулярна одній стороні кута і паралельна другій.
Лобачевський довів, що між множиною всіх гострих кутів 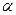 і множиною додатних дійсних чисел
і множиною додатних дійсних чисел 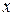 існує бієктивна відповідність і знайшов її явний вигляд, який називають тепер функцією Лобачевського (або основною формулою Лобачевського) і позначають
існує бієктивна відповідність і знайшов її явний вигляд, який називають тепер функцією Лобачевського (або основною формулою Лобачевського) і позначають 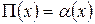 . Вона має вигляд
. Вона має вигляд
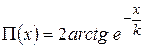 або
або 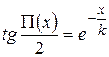 ,
,
де 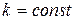 називається константою Лобачевського або радіусом кривини. З рівностей
називається константою Лобачевського або радіусом кривини. З рівностей 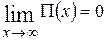 ,
, 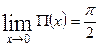 випливає, що зі збільшенням відрізка паралельності відмінність геометрії Лобачевського від геометрії Евкліда стає все більшою, і, навпаки, в достатньо малому околі площини Лобачевського виконується геометрія Евкліда (або, геометрія Евкліда є граничним випадком геометрії Лобачевського).
випливає, що зі збільшенням відрізка паралельності відмінність геометрії Лобачевського від геометрії Евкліда стає все більшою, і, навпаки, в достатньо малому околі площини Лобачевського виконується геометрія Евкліда (або, геометрія Евкліда є граничним випадком геометрії Лобачевського).
Теорема.Нехай 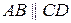 і
і 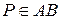 . Якщо точка
. Якщо точка 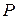 рухається по прямій в сторону паралельності, то її відстань до прямої
рухається по прямій в сторону паралельності, то її відстань до прямої 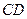 прямує до нуля. Якщо ж точка
прямує до нуля. Якщо ж точка 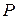 рухається по прямій
рухається по прямій 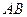 в протилежному напрямку, то її відстань до прямої
в протилежному напрямку, то її відстань до прямої 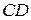 необмежено збільшується.
необмежено збільшується.
Доведенняскладається з двох частин. Спочатку доводиться, що при умові 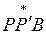 , де
, де 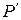 - нове положення точки
- нове положення точки 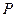 виконується
виконується 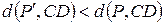 , а потім – що
, а потім – що 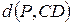 може стати менша за будь-яке як завгодно мале додатне дійсне число
може стати менша за будь-яке як завгодно мале додатне дійсне число 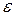 .
.
Наслідок.Будь-яка пара паралельних прямих може за допомогою руху накладена на іншу пару паралельних прямих.
Означення.Дві різні прямі називаються розбіжними, якщо вони не перетинаються і не паралельні.
Теорема.Розбіжні прямі існують.
Наприклад, розбіжними є два перпендикуляри до однієї прямої.
Теорема (ознаки розбіжності прямих). Дві різні прямі є розбіжними тоді і тільки тоді, коли при перетині цих прямих третьою утворюються або рівні відповідні кути, або рівні навхрест лежачі кути, або внутрішні односторонні кути, сума яких дорівнює 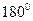 .
.
Дата добавления: 2016-12-08; просмотров: 4726;
