В) Обґрунтування теорії вимірювання відрізків за допомогою аксіом четвертої групи. Поняття абсолютної геометрії.
Дотепер ми порівнювали відрізки або кути за допомогою неозначуваного поняття третьої групи «конгруентність». Для введення поняття довжини відрізка аксіом перших трьох груп недостатньо. Аксіоми Архімеда і Кантора системи Гільберта дозволяють обґрунтувати теорію вимірювання відрізків і кутів. В системі аксіом Погорєлова евклідового простору (додаток В) в четвертій групі є лише одна аксіома – Дедекінда. Виявляється, що аксіома Дедекінда еквівалентна сукупності аксіом Архімеда і Кантора. Доведення відповідних теорем можна знайти, наприклад, в книзі [8].
Задача вимірювання довжин відрізків полягає в тому, щоб задати відношення будь-якого відрізка до деякого фіксованого відрізка дійсним числом. Цей фіксований відрізок називають лінійною одиницею (або одиницею вимірювання довжин).
Означення. Нехай задана відповідність, при якій кожному відрізку зіставляється певне додатне число так, що:
1. конгруентним відрізкам відповідають рівні числа;
2. якщо В – внутрішня точка відрізка АC та відрізку AB відповідає число а, а відрізку ВС відповідає число b, то відрізку AC буде відповідати число a+b;
3. існує відрізок, якому відповідає число 1.
Тоді число, що відповідає відрізку, називається його довжиною.
Таке означення вимагає доведення його коректності. В аксіоматичній теорії за Гільбертом, викладеній в книзі [8] це зроблено наступним чином. Спочатку із припущення існування такої відповідності доводиться, що вона єдина, тобто доводиться
Теорема. Якщо вказана в означенні відповідність існує та задовольняє умовам 1, 2, 3, то вона єдина.
Далі доводиться
Теорема. Вказана у визначенні відповідність існує та задовольняє умовам 1, 2 та 3.
Важливим моментом в доведенні останньої теореми є використання аксіоми Архімеда. Фактично доведення є певною мірою конструктивним, оскільки містить описання процесу, який дозволяє для обраного відрізка знаходити відповідне йому додатне дійсне число.
Але відомий в евклідовій геометрії факт, що довжини всіх відрізків вичерпують всі додатні дійсні числа, не випливає з аксіом перших трьох груп і аксіоми Архімеда. Тому далі доводиться
Теорема.Для будь-якого дійсного числа 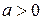 існує відрізок, довжина якого дорівнює
існує відрізок, довжина якого дорівнює 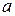 .
.
При доведенні цієї теореми використовується друга з аксіом неперервності – аксіома Кантора.
Аналогічні міркування потрібні для введення поняття величини кута. Якщо одиницю вимірювання кутів вибрати так, щоб прямому куту відповідало число 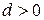 , то між множиною всіх кутів і множиною всіх дійсних чисел з інтервалу
, то між множиною всіх кутів і множиною всіх дійсних чисел з інтервалу 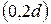 встановлюється взаємно однозначна відповідність. Прийнято одиницю вимірювання кутів вибирати так, щоб прямому куту відповідало дійсне число
встановлюється взаємно однозначна відповідність. Прийнято одиницю вимірювання кутів вибирати так, щоб прямому куту відповідало дійсне число  .
.
Після обґрунтування процесу вимірювання відрізків і кутів з’являється можливість користуватись в геометрії алгеброю. Зокрема, можна ввести систему координат на прямій, на площині, в просторі. А введення координат на прямій, в свою чергу, дозволяє сформулювати наступну важливу теорему.
Теорема.Між впорядкованою множиною всіх точок прямої і впорядкованою множиною всіх дійсних чисел існує така взаємно однозначна відповідність, при якій відповідні елементи знаходяться у відповідних відношеннях порядку.
Зауваження. Вказана властивість прямої називається неперервністю. Також ця теорема показує ізоморфізм двох моделей однієї математичної структури, яку називають лінійним порядком.
Абсолютною геометрією називається аксіоматична теорія, побудована на перших чотирьох групах аксіом Гільберта.
Прикладами теорем абсолютної геометрії є всі теореми з номерами 1– 46 аксіоматичної теорії, викладеної в книзі [8] (див. також Додаток Г). Наведемо ще список важливих теорем абсолютної геометрії, які були доведені в роботах Саккері, Лежандра, Ламберта в ході їх досліджень, пов’язаних з проблемою п’ятого постулату.
Теорема.Сума всіх внутрішніх кутів довільного трикутника не перевищує 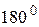 .
.
Теорема.Якщо сума кутів хоча б одного трикутника дорівнює двом прямим кутам, то сума кутів будь-якого трикутника дорівнює двом прямим кутам.
Теорема.Якщо в даному трикутника сума всіх внутрішніх кутів дорівнює 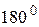 і цей трикутник ділиться трансверсаллю на два трикутники, то сума внутрішніх кутів кожного з цих трикутників теж дорівнює
і цей трикутник ділиться трансверсаллю на два трикутники, то сума внутрішніх кутів кожного з цих трикутників теж дорівнює 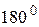 .
.
Теорема.Якщо існує трикутник, в якому сума всіх внутрішніх кутів не перевищує 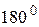 , то і в будь-якому трикутнику сума внутрішніх кутів не перевищує
, то і в будь-якому трикутнику сума внутрішніх кутів не перевищує 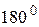 .
.
Дата добавления: 2016-12-08; просмотров: 1489;
