Означення перерізу на множині раціональних чисел. Приклади перерізів.

Означення.Перерізом впорядкованої множини М є представлення цієї множини у вигляді 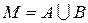, де підмножини 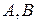називають класами і вони мають властивості:

1) кожний клас непорожній;

2) кожний елемент множини М належить тільки одному з класів;

3) якщо 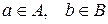, то .

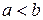Переріз позначають символом .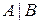

Наведемо приклади різних перетинів у множині раціональних чисел.

1 вид перетину: лівий клас має найбільше число, а правий – не має найменшого числа. Наприклад, .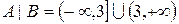

2 вид перетину: лівий клас не має найбільшого числа, а правий – має найменше число. Наприклад,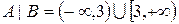

3 вид перетину: лівий клас не має найбільшого числа, а правий – не має найменшого числа.

Доведемо, що такий переріз можливий на множині раціональних чисел.

До класу А віднесемо всі від’ємні раціональні числа, число 0 та всі додатні раціональні числа, квадрат яких менший 2, до класу В – всі інші раціональні числа. Тоді

1) кожен клас непорожній;

2) будь-яке число з класу А менше за будь-яке число з класу В.

Припустимо, що число 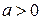є найбільшим в класі А. Розглянемо число 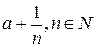і покажемо, що існує таке 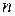, що 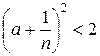. Дійсно, 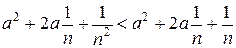. Нерівність 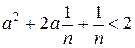справедлива для натуральних 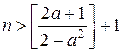. Значить, при таких 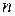виконується і нерівність 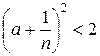. Це означає, що число 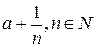належить до класу А, але, оскільки воно більше числа 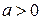, то 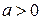не є найбільшим в класі А.

Припустимо тепер, що число 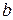найменше в класі В. Розглянемо число 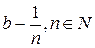та покажемо, що існує 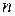таке, що 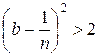. Оскільки 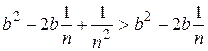, то нерівність 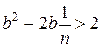справедлива для натуральних 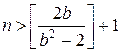. Значить при таких 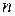виконується і нерівність 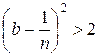. Це означає, що число 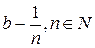належить до класу В, але, оскільки воно менше числа 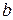, то 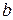не є найменшим в класі В.

Висновок: побудований переріз є перерізом третього виду.