Граница абсолютной погрешности частного двух приближенных чисел равна произведению границы относительной погрешности частного на модуль частного этих чисел.
х = а ± h а 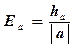
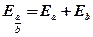
у = b ± h b 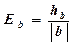
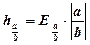
Пример:
1. Найти абсолютную и относительную точность частного приближенных значений х = 13,496 ± 0,01 и у = 4,73 ± 0,03.
Решение:
1) Определить верные и сомнительные цифры приближенных значений х, у:
 х = 13,496 ± 0,01
х = 13,496 ± 0,01
Цифра 6 в 0,001; h а = 0,01 £ 0,001; 6 – сомнительная цифра;
Цифра 9 в 0,01; h а = 0,01 £ 0,01; 9 – верная цифра;
Следовательно, 4; 3; 1 – верные цифры.
13,496 » 13,50; D х = |13,496 – 13,50| = 0,004;
х = 13,50 ± (0,01+ 0,004); х = 13,50 ± 0,014;
 у = 4,73 ± 0,03
у = 4,73 ± 0,03
Цифра 3 в 0,01; h а = 0,03 £ 0,01; 3 – сомнительная цифра;
Цифра 7 в 0, 1; h а = 0,03 £ 0,1; 7 – верная цифра;
Следовательно, 4 – верная цифра.
4,73 » 4,7; D у = |4,73 – 4,7| = 0,03;
у = 4,7 ± (0,03+ 0,03); у = 4,7 ± 0,06.
2) Найти частное приближенных значений х = 13,50 ± 0,014 и
у = 4,7 ±0,06:
х : у = 13,50 : 4,7 = 2,8723…» 2,9;
3) Найти абсолютную и относительную точность частного приближенных значений х и у:
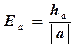
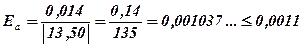
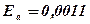
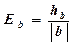
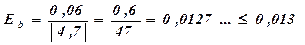
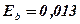
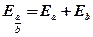
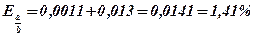
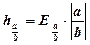
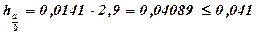
Ответ: х : у = 2,9 ± 0,041 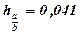
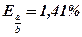
Правило №4
Граница относительной погрешности степени приближенного числа равна произведению границы относительной погрешности основания на показатель степени.
Граница абсолютной погрешности степени приближенного числа равна произведению границы относительной погрешности степени приближенного числа на модуль степени.
х = а ± h а ; п – показатель степени;
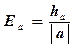
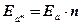
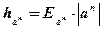
Правило №5
Граница относительной погрешности корня из приближенного числа равна границе относительной погрешности подкоренного числа, деленной на показатель корня.
Граница абсолютной погрешности корня из приближенного числа равна границе относительной погрешности корня из приближенного числа, умноженной на модуль корня из приближенного числа.
х = а ± h а ; п – показатель корня;
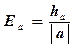
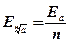
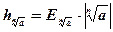
Пример:
1. Определить куб приближенного значения числа х = 2,39 ± 0,03, границы абсолютной и относительной погрешностей куба приближенного значения числа х.
Решение:
Дата добавления: 2017-01-29; просмотров: 4666;
