Относительная погрешность, граница относительной погрешности являются безразмерными величинами.
Определение: Границей относительной погрешности приближения называется положительное число Е, которое больше или равно самой относительной погрешности.
; 
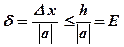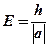
Пример:
1. Сравнить качество двух измерений:
а) длина предмета а1= 1,2 м , D х1= 0,005 м;
б) расстояние а2 = 6,76 км , D х2 = 10 м .
Решение:
При первом измерении допущена погрешность D х1 = 0,005 м = 5 мм на 1,2 м =
= 1200 мм. Определим относительную погрешность первого измерения, то есть какую часть (сколько %) составляет абсолютная погрешность Dх1 от приближенного значения а1 .
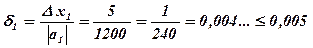;Е1 = 0,005 = 0,5 % .
Определим относительную погрешность второго измерения, то есть какую часть (сколько %) составляет абсолютная погрешность Dх2 = 10 м от приближенного значения а2 = 6,76 км = 6760 м .
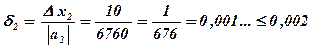;Е2 = 0,002 = 0,2 % .
Е2 £ Е1 , следовательно, качество второго измерения лучше.
Ответ: Качество второго измерения лучше.
2. Термометр дает отклонение не более 0,5° С . Им измерили температуру воздуха и получили 17° С . С какой относительной точностью выполнено измерение?
а = 17° С Под относительной точностью понимается граница
h = 0,5° С относительной погрешности данного измерения.
Е = ?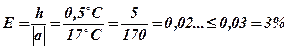 
;Е = 3 % .
Ответ: Е = 3 % .
Упражнения:
1. Сравнить качество двух измерений:
а) масса железнодорожного вагона т1 = 63 ± 0,5(т);
б) масса дозы лекарства т2 = 0,15 ± 0,005(г).
2. Определить границу относительной погрешности следующих чисел:
а) а = 142,5; D х = 0,05; г) а = 2,372; D х = 0,004;
б) а = 6,93; D х = 0,02; д) а = 12,79; D х = 2.
3. Найти границу абсолютной погрешности числа а = 1348, если Е = 0,04 %.
4. Известно, что х » а с точностью до Е %. Найти границу абсолютной погрешности приближения, если:
а) а = 2,75; Е = 20 %; в) а = 237; Е = 1 %;
б) а = 1,3; Е = 10 %; г) а = 1,49; Е = 0,1 %.
Дата добавления: 2017-01-29; просмотров: 9209;