Если приближенное значение числа записано в стандартном виде, то все верные цифры будут и значащими.
3. Граница абсолютной погрешности приближенного значения числа, записанного в стандартном виде а × 10 к, равна единице разряда последней сохраняемой цифры, умноженной на 10 к.
Пример: d Солнца = 1390600000 м = 1,3906 × 10 9 м , к = 9, h = 0,0001 × 10 9 = 10 5;
d молекулы воды = 0,00000003 см = 3 × 10 – 8 см , к = – 8, h = 1 × 10 – 8 = 10 – 8 ;
m Земли = 5,98 × 10 24 кг , к = 24, h = 0,01 × 10 24 = 10 22;
v света = 2,99793× 10 8 м / с , к = 8, h = 0,00001 × 10 8 = 10 3.
Пример:
1. Записать правильно приближенное значение числа х = 9,846 ± 0,04.
Решение:
1) 
Определить верные и сомнительные цифры в приближенном значении числа х:
Цифра 6 в 0,001; h = 0,04 £ 0,001 , 6 – сомнительная цифра;
Цифра 4 в 0,01; h = 0,04 £ 0,01 , 4 – сомнительная цифра;
Цифра 8 в 0,1; h = 0,04 £ 0,1 , 8 – верная цифра;
Следовательно, 9 – верная цифра.
2) Округлить данное приближенное значение 9,846 числа х, сохраняя только верные цифры: 9,846 ≈ 9,8 .
3) Найти ошибку округления: D х = ½9,846 – 9,8½ = 0,046.
4) Определить границу абсолютной погрешности нового приближенного значения 9,8 числа х: х = 9,8 ± (0,04 + 0,046) = 9,8 ± 0,086 .
Ответ: х = 9,8 ± 0,086 .
2. Записать правильно приближенное значение числа х = 1,23 ± 0,02.
Решение:
1) Определить верные и сомнительные цифры в приближенном значении 1,23:
Цифра 3 в 0,01; h = 0,02 £ 0,01 , 3 – сомнительная цифра;
Цифра 2 в 0,1; h = 0,02 £ 0,1 , 2 – верная цифра;
Следовательно, 1 – верная цифра.
2) Округлить данное приближенное значение 1,23 числа х , сохраняя только верные цифры: 1,23 ≈ 1,2 .
3) Найти ошибку округления: D х = ½1,23 – 1,2½ = 0,03.
4) Определить границу абсолютной погрешности нового приближенного значения 1,2 числа х: х = 1,2 ± (0,02 + 0,03) = 1,2 ± 0,05 .
Ответ: х = 1,2 ± 0,05 .
Вывод: При округлении приближенного значения числа граница абсолютной погрешности увеличивается на ошибку округления.
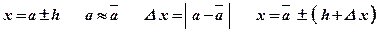
а – данное приближенное значение числа х ;
h – граница абсолютной погрешности данного приближенного значения а ;
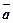– новое приближенное значение числа х ;
D х – ошибка округления;
h + D х – граница абсолютной погрешности нового приближенного значения .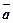
Упражнения:
- Округлить с точностью до 10 – 2 (сотых) данные числа:
а) 0,428; в) 16,452; д) 22,1488; ж) 8,993;
б) 2,645; г) 25,689; е) 62,8428; з) 17,8975.
- Округлить с точностью до 1(единиц) данные числа:
а) 16,285; в) 60,605; д) 31,499; ж) 193,13;
б) 785,507; г) 2,501; е) 0,499; з) 22999, 84.
- с точностью до 1000 (тысяч) данные числа:
а) 1835; г) 10428; ж) 4172,035; к) 199833,1;
л) 791,5; е) 16765; и) 1335,42; м) 29393.
- Округлить до первого справа верного разряда приближенные значения чисел. Результат округления записать в стандартном виде.
а) х = 0,3281 ± 0,05; в) х = 12378 ± 25; д) х = 8764 ± 25;
б) х = 2,0637 ± 0,0025; г) х = 14,0367 ± 0,8; ё е) х = 812 ± 6.
- Указать границу абсолютной погрешности приближенного числа, если в записи его все цифры верные:
а) х » 0,56; в) х » 153,100; д) х » 9,30 × 10 – 3;
б) х » 84,3; г) х » 7,123 × 10 4; е) х » 3,567 × 10 – 1
- Найти границу относительной погрешности приближенного числа, если в записи его все цифры верные: а) х » 6,8; б) у » 13,08.
- Какие цифры приближенного значения 4,86 числа х являются верными, если граница относительной погрешности приближения равна 0,3 %?
- Записать в стандартном виде следующие числа:
а) 0,523; в) 302,25; д) 0,40 × 10 – 2; ж) 193,1× 10 – 3;
б) 0,031; г) 37,4 × 10 3; е) 3785,5; з) 42799, 8.
- Определить порядки следующих чисел: а) 0,3; б) 321,24; в) 5 × 10 5; г) 47,5 × 10 – 3; д) 3,51; е) 21; ж) 0,1× 10 – 2; з) 42799, 8 × 10 3.
- Сколько значащих цифр в приближенных числах: 2,718; 10,209; 0,091; 0,000302?
- Указать значащие цифры приближенных значений чисел:
а) х = 2,10 ± 0,02; б) z = 1,5 × 10 3± 10 2; в) у = 20,1 ± 0,1.
Дата добавления: 2017-01-29; просмотров: 6077;