Определить верные и сомнительные цифры приближенного значения числа

Цифра 9 в 0,01; h _а = 0,03 £ 0,01; 9 – сомнительная цифра;

Цифра 3 в 0,1; h _а = 0,03 £ 0,1; 3 – верная цифра;

Следовательно, 2 – верная цифра.

2,39 » 2,4; D х = |2,39 – 2,4| = 0,01;

х = 2,4 ± (0,03+ 0,01); х = 2,4 ± 0,04;

2) Найти куб приближенного значения числа х = 2,4 ± 0,04:

х ³» 2,4 ³ = 13,824 » 14;

3) Найти границу относительной погрешности приближенного значения 2,4:

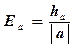
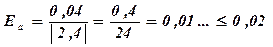
4) Найти границу абсолютной и относительной погрешностей куба приближенного значения числа х:

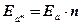
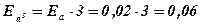
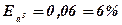
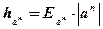
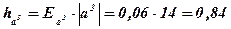
Ответ: х ³ = 14 ± 0,84;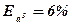

2. Определить границу абсолютной погрешности кубического корня из приближенного значения 39,7 числа х, данного с точностью до 1,5 % .

х » 39,7; Е_а = 1,5 % = 0,015.

Решение:

;

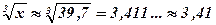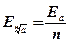
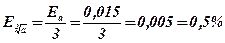
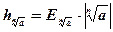
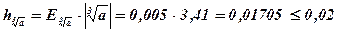
Ответ: .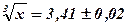

Упражнения:

1. Найти сумму х + у и разность х- у, если:

а) х = 7,8 ± 0,05; у = 3,4 ± 0,05; б) х = 1,25 ± 0,05; у= 1,02 ± 0,02;

2. Найти произведение ху и частное 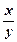, если:

а) х » 3,2 с точностью до 0,5 % , у » 2,35 с точностью до 1 %;

б) х » 3,5 с точностью до 1 % , у » 1,23 с точностью до 0,5 %;

в) х» 0,43 с точностью до 0,1 % , у » 4,3 с точностью до 1 %.

3. Известно, что ребро куба измерено с точностью до 0,5 %. С какой точностью будет вычислен объем куба?

4. Какая разница между записями температуры 18° С и 18,0° С?

5. Какое из двух измерений точнее: х = 895 ± 0,5 (м); у = 24,08 ± 0,01 (м).

6. Написать число 18,754 без лишних цифр, зная, что относительная погрешность его равна 0,5 %.

7. Найти границу относительной погрешности результатов, записанных в стандартном виде:

а) плотность ртути 1,361 · 10 ¹ г / см³; в) плотность воды 1,00 · 10 ⁰ г / см³;

б) плотность молока 1,03 · 10 ⁰ г / см³; г) плотность воздуха 1,29 · 10 ^{– 3} г / см³.

8. Найти сумму приближенных чисел, границу абсолютной погрешности и границу относительной погрешности суммы приближенных чисел, если: