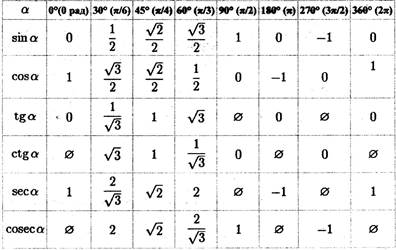
6 страница. Функция у = f (х) называется чётной, если значение у не изменяется при замене х на -х, т.е
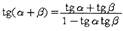
|
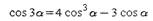
|
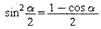
|
Функция у = f (х) называется чётной, если значение у не изменяется при
замене х на -х, т.е. функция у =f(х) называется чётной, если f(-x) = f(x)
• Функции cos α, sec α, - чётные функции, a sin α, tg α, ctg α, cosec α -
нечётные.
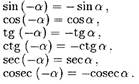
|
Формулы сложения:
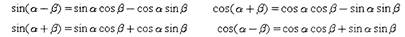
|
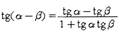
|
Формулы двойного и тройного угла:
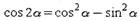
|
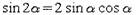
|
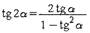
|
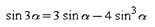
|
Формулы понижения степени:
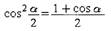
|
Формулы приведения:
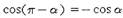
|
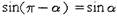
|
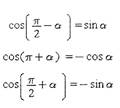
|
Наиболее употребительными являются следующие формулы: Формулы суммы и разности синусов:
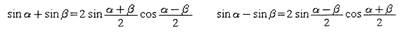
|
Формулы суммы и разности косинусов:
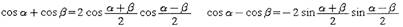
|
Формулы суммы и разности тангенсов:
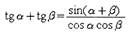
|
Преобразование произведения синусов и косинусов в сумму (разность):
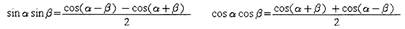
|
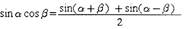
|
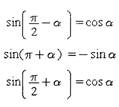
|
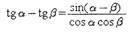
|
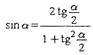
|
Выражение синуса и косинуса через тангенс половинного аргумента:
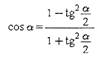
|
|
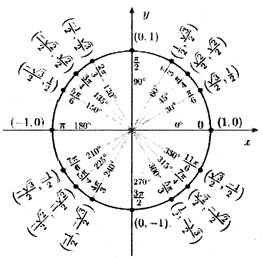
Значения косинуса и синуса на окружности.
|
причем известен закон изменения переменной хп , т.е. для каждого
натурального числа п можно указать соответствующее значение хn. Таким
образом предполагается, что переменная хn является функцией от n:
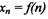
|
Определение. Постоянное число а называется пределом
последовательности x1 ,x2,...,хп,.... или пределом переменной хп , если для
сколь угодно малого положительного числа ε найдется такое натуральное
число N (т.е номер N), что все значения переменной xn , начиная с xn,
отличаются от а по абсолютной величине меньше, чем на ε. Данное
определение кратко записывается так:
Здесь п→ ∞ означает, что п неограниченно возрастает. Часто говорят
также: хn стремится к а и пишут xn→а.
Таким образом, переменная хn имеет предел а, если абсолютная величина
разности между хn и а в процессе изменения переменной хп, пробегающей
последовательность x1 , х2,..., xn, становится (в момент, когда п = N) и в
дальнейшем остается (т.е. для всех п > N) меньше заданного положительного
числа ε.
Чем меньшим будет выбрано ε, тем большим будет число N. При n>N
выполняется неравенство (2), но для того, чтобы число а было пределом
переменной хn необходимо, чтобы такое число N нашлось, как бы ни мало
было число ε.
Но не всякая переменная имеет предел. Так, переменная хn , принимающая
последовательно значения
| Предел последовательности |
Пусть переменная величина хn принимает бесконечную последовательность значений
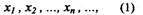
|

|
| при всех n ≥ N, или, что то же самое, |
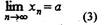
|

| Рассмотрим пример, когда Тогда не существует такого номера N, что для n ≥ N всегда выполнялось бы равенство |
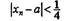
|
1, 0, 1, 0,..., 1, 0,...,
предела не имеет, так как в данном случае для любого постоянного числа
Теорема. Переменная хn может иметь только один предел.
(без доказательства)
Арифметическая прогрессия
Арифметическая прогрессия - арифметический ряд первого порядка -
последовательность чисел, в которой каждый член (начиная со второго)
получается из предыдущего путем прибавления к нему одного и того же
числа называемого разностью этой арифметической прогрессии.
Каждая арифметическая прогрессия имеет вид а, а + d, а + 2d, а + 3d, ...
Общий член арифметической прогрессии аn = а1 + d(n - 1)
Характеристическое свойство арифметической профессии
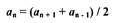
|
Если разность арифметической прогрессии d > 0, то прогрессия называется
возрастающей, если d < 0 - убывающей.
Простейший пример арифметической прогрессии - натуральный ряд чисе;
1,2,3,..., n,...
Число членов арифметической прогрессии может быть ограниченным либо
неограниченным.
Если арифметическая прогрессия содержит n членов, то ее сумму можно
вычислить по формуле Sn = (a1 + аn)*п /2
Пример: 1, 3, 5, 7, 9, 11, 13... - арифметическая прогрессия.
Геометрическая прогрессия
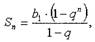
|
Геометрическая прогрессия - числовая последовательность, каждый член
которой, начинается со второго, равен предыдущему, умноженному на
некоторое отличное от нуля постоянное число.
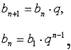
|
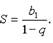
|
для бесконечно убывающей прогрессии
Пример: 2, 8, 32,128,..., - геометрическая прогрессия. Постоянное число q,
называется знаменателем геометрической профессии: q = 4.
Пример: Закон Вебера — Фехнера — открытый Э.Г.Вебером и развитый
Г.Т.Фехнером - основной психофизиологический закон, согласно которому
при увеличении силы воздействия в геометрической прогрессии (1, 2, 4, 8,
16 и т.д.) интенсивность ощущения увеличивается в арифметической
прогрессии (0, 1, 2, 3, 4 и т.д.);
Дополнительный список интегралов (первообразных функций)
Интегралы от экспоненциальной функции.

|

|
| Интегралы, содержащие только sin |
| (n >0) |
Интегралы, содержащие только cos
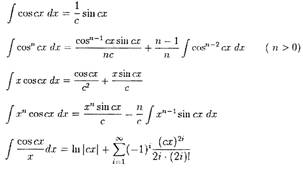
|
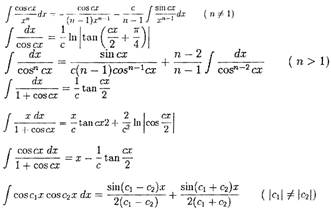
|
ИНФОРМАЦИЯ ДЛЯ ПОДГОТОВКИ К ПРАКТИЧЕСКИМ ЗАНЯТИЯМ
При составлении данного пособия использовались материалы, которые при
желании можно просмотреть в оригинале, соответственно следующему
списку литературы:
1. «Основы высшей математики» Шипачёв B.C. Издательство:
Юрайт.2009
2. «Математика» Башмаков М.И. Учебник для 10-11 классов. (Для тех,
кто забыл школьный курс) Издательство: Academia. 2008
3. «Алгебра и начала анализа. 11 класс. В 2-х частях. Мордкович
А.Г., Семенов П.В. Учебник. Издательство: Мнемозина. 2008г.
4. «Сборник задач по медицинской и биологической физике». А.Н.
Ремизов и др. Издательство: Дрофа. 2008
5. Краткий курс высшей математики для биологических и
медицинских специальностей. Баврин И.И. 2003.
6. Сборник задач по алгебре и началам анализа. Учебное пособие.
Карп А. П.
7. Сборник задач по высшей математике: Учебное пособие. Бугров
Я. С., Никольский С. М.
Дополнительные источники информации для самостоятельной работы:
1.Математические модели в биологии. Электронная библиотека CD-
ROM, 2006 г. Издатель: R&C Dynamics; Разработчик: R&C Dynamics
2. Математические модели в биофизике и экологии. Ризниченко Г.Ю.
2003.
3. МАТЕМАТИКА В БИОЛОГИИ И МЕДИЦИНЕ. Н.Бейли
Дата добавления: 2016-06-24; просмотров: 2458;
