Аддитивные и мультипликативные погрешности

Любое средство измерений обладает статической характеристикой, т.е. характеристикой, функционально связывающей выходную величину Y c входной величиной X. Обычно статическая характеристика является линейной. При отсутствии погрешностей для нее справедливо соотношение

,

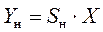где Y_н – номинальная статическая характеристика средства измерения; S_н – номинальная чувствительность средства измерения.

Наличие погрешности средства измерения вызывает изменение чувствительности (S_н+DS), а также смещение результата измерения на величину D_а, т.е.

Y = (S_н+DS) × X + D_а.

Погрешность DY результата измерений при этом определится как

DY = Y – Y_н = DS × X+D_а.

Первая составляющая погрешности является мультипликативной (D_м = DS × X), а вторая – аддитивной (D_а = D_а).

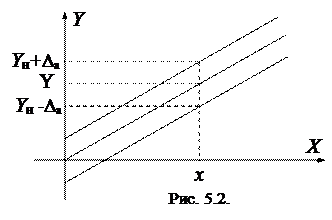Дадим определение аддитив-ной и мультипликативной погреш-ностям.

Аддитивной называется погрешность абсолютное значение которой неизменно во всем диапазоне измеряемой величины.

Систематическая аддитивная погрешность смещает номинальную характеристику параллельно вверх или вниз на величину ±D_а (рис. 5.2).

Примером систематической аддитивной погрешности может служить погрешность от неточной установки прибора на нуль, от контактной э.д.с. в цепи постоянного тока. Аддитивную погрешность еще называют погрешностью нуля.

Мультипликативной называют погрешность абсолютное значение которой изменяется пропорционально измеряемой величине.

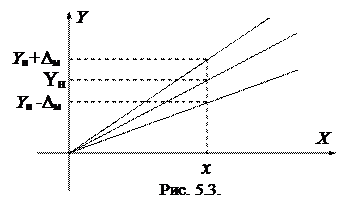При систематической мульти-пликативной погрешности реальная характеристика отклоняется от но-минальной вверх или вниз (рис.5.3).

Примерами систематических мультипликативных погрешностей являются погрешности из-за изменения коэффициента деления делителя напряжения, из-за изменения жесткости пружины измерительного механизма и т.п. Мультипликативную погрешность еще называют погрешностью чувствительности.

В средствах измерения аддитивные и мультипликативные погрешности, как правило, присутствуют одновременно. В этом случае результирующая погрешность определяется суммой аддитивной и мультипликативной погрешностей D = D_а+D_м= D_а+ d_м × Х, где d_м – относительная мультипликативная погрешность. В зависимости от соотношений аддитивной (D_а) и мультипликативной (D_м) погрешностей классы точности средств измерений обозначаются по-разному. Можно выделить три характерных случая соотношения этих погрешностей 1) D_а = 0, D_м ¹ 0; 2) D_а ¹ 0, D_м = 0; 3) D_а @ D_м.