И результата измерений

Рассчитывая значения погрешности, особенно при использовании электронного калькулятора, получают значения с большим числом знаков. Однако исходными данными для расчета являются нормируемые значения погрешности средства измерений и класс точности, которые указываются всего с одной или двумя значащими цифрами. Вследствие этого и в окончательном значении рассчитанной погрешности должны быть оставлены только первые (одна или две) значащие цифры.

При этом приходится учитывать следующее обстоятельство. Если полученное число начинается с цифр 1 или 2, то отбрасывание второго знака приведет к очень большой ошибке (до 30–50 %), что недопустимо. Если же полученное число начинается, например, с цифры 9, то сохранение второго знака, т.е. указание погрешности, например, 0,94 вместо 0,9, является дезинформацией, т.к. исходные данные не обеспечивают такой точности.

Исходя из этого, на практике установилось следующее правило: если полученное число начинается с цифры равной или большей, чем 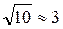, то в нем сохраняется лишь один знак. Если же оно начинается с цифр, меньших 3, т.е. с цифр 1 и 2, то в нем сохраняют два знака.

На основании вышеизложенного можно сформулировать следующие три правила округления рассчитанного значения погрешности и полученного экспериментального результата измерения.

Правило 1. Погрешность результата измерения указывается двумя значащими цифрами, если первая их них равна 1 или 2, и одной – если первая цифра равна 3 и более.

Правило 2. Результат измерения округляется до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности.

Правило 3. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним - двумя лишними знаками.

Пример.На вольтметре класса точности 2,5 с пределом измерения 300 В был получен отсчет измеряемого напряжения х = 267,5 В. Определить абсолютную и относительную погрешности измерения, произвести округление их значений и округление результата измерения. Представить результат измерения.

Решение. Здесь класс точности указан числом без кружочка, следовательно, абсолютную погрешность находим по формуле

,

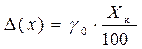где g₀ = 2,5, а Х_к = 300 В.

Тогда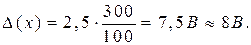

Так как 7 > 3, то D(х) округляем до 8 В.

Относительная погрешность определится по формуле

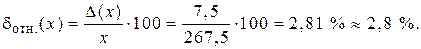
Так как 2 < 3, то в ответе должны быть сохранены два десятичных разряда, поэтому d_отн.(х) округляем до 2,8 %.

Далее необходимо округлить полученное значение напряжения х = 267,5 В. Оно должно быть округлено (см. правило 2) до того же десятичного разряда, которым оканчивается округленное значение абсолютной погрешности, т.е. до целых единиц вольт x = 267,5 В » 268 В.

Представление результата.Измерение произведено с относительной погрешностью d_отн.(х) = 2,8 %. Измеренное напряжение х = 268 В лежит в интервале неопределенности

260 В < х < 276 В.

6.3. Правила приближенных вычислений

В приближенных и точных числах значащими цифрами (знаками) называют все цифры: 1, 2, 3, 4, 5, 6, 7, 8, 9, цифра 0 тоже является значащей, если она стоит в середине числа или на его конце. Например, в числах 250; 205; 20500; 20,5; 2,005; 20,00 все цифры являются значащими. Нуль не является значащей цифрой, если он стоит с левой стороны в десятичной дроби, т. к. в этом случае от него не зависит значность числа, выраженного десятичной дробью. Например, 0,23; 0,039; 0,0365; 0,0033.

Верными знаками являются те, за точность которых можно ручаться. В приближенном числе последняя цифра (справа) не является точной и называется сомнительной. Например, в приближенном числе l = 13,84 мм, погрешность которого 0,01 мм, цифра 4 (сотые доли) сомнительна, т.к. истинное значение числа лежит в интервале от (13,84 – 0,01) до (13,84 + 0,01) мм. Таким образом, в приближенном числе сомнительная цифра принадлежит к тому же разряду, что и разряд первой (слева) значащей цифры в абсолютной ошибке. Тогда в приближенном числе 943, имеющем абсолютную погрешность 21, цифра 4 сомнительна, а цифра 3 подавно сомнительна и ее надо заменить нулем. Не отбросить, а заменить, чтобы сохранить значность данного приближенного числа. Итак, 940±20, или (94±2) ×10. В приближенном числе 27,352, имеющем абсолютную погрешность 0,01, цифра 5 сомнительна, а цифра 2 подавно сомнительна, но ее можно отбросить, т.к. значность числа не изменится. Итак, 27,35±0,01.

Приближенные вычисления следует вести с соблюдением следующих правил.

1. При сложении и вычитании приближенных чисел окон­чательный результат округляют так, чтобы он не имел значащих цифр в тех разрядах, которые отсутствуют хотя бы в одном из при­ближенных данных.

Например, при сложении чисел

4,462 + 2,38 + 1,17273 + 1,0262 = 9,04093 следует сумму округлить до сотых долей, т.е. принять ее равной 9,04.

2. При умножении следует округлять сомножители так, чтобы каждый из них содержал столько значащих цифр, сколько их имеет сомножитель с наименьшим числом таких цифр.

Например, вместо вычисления выражения

3,723 × 2,4 × 5,1846

следует вычислять выражение

3,7 × 2,4 × 5,2.

В окончательном результате следует оставлять такое же число значащих цифр, какое имеется в сомножителях после их округления.

В промежуточных результатах следует сохранять на одну значащую цифру больше. Такое же правило следует соблюдать и при делении приближенных чисел.

3. При возведении в квадрат или в куб следует в степени брать столько значащих цифр, сколько их имеется в основании степени.
Например,

1,32² » 1,74.

4. При извлечении квадратного или кубического корня в результате следует брать столько значащих цифр, сколько их имеется в подкоренном выражении. Например,

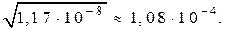
5. При отбрасывании сомнительных цифр следует помнить:

- если отбрасываемая (n + 1) цифра меньше 5, то остающаяся n-я цифра не меняется (пример: 10,132 после округления 10,13);

- если отбрасываемая (n + 1) цифра равна или больше 5, то остающаяся n-я цифра увеличивается на 1 (пример: 9,836 после округления 9,84).

ЛЕКЦИЯ 7