Виды и методы измерений

В зависимости от способа получения измеряемой величины измерения делят на 4 вида: прямые, косвенные, совместные и совокупные.

Прямые измерения заключаются в экспериментальном сравнении измеряемой величины с мерой этой величины или в отсчете показаний измерительного прибора, непосредственно дающего значение измеряемой величины.

Результат косвенных измерений получают на основании прямых измерений величин, связанных с измеряемой величиной известной зависимостью. Например, определение объема тел правильной геометрической формы по результатам прямых измерений его линейных размеров и соответствующего математического расчета. То же относится и к определению плотности материалов, предела прочности при сжатии.

Совместными называют производимые одновременно измерения двух или нескольких неодноименных величин для нахождения зависимости между ними. При этом значения измеряемых величин находят по данным повторных прямых или косвенных измерений неодноименных величин. Повторные измерения проводят при различных сочетаниях мер либо при изменяющихся условиях, что дает возможность составить систему уравнений, решив которую, находят искомое значение измеряемой величины. Такой метод, например, используют при определении модуля упругости бетона.

Совокупными называют производимые одновременно измерения нескольких одноименных величин, при которых искомые значения находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.

Разновидности прямых измерений:

- метод непосредственной оценки; - дифференциальный метод;

- нулевой метод;

- метод совпадений.

Метод непосредственной оценки позволяет получить значение величины непосредственно, без каких-либо дополнительных действий и без вычислений (исключение - умножение показаний на постоянную прибора или на цену деления). Такие измерения производят на манометрах, динамометрах, жидкостных термометрах, взвешивание на циферблатных весах, измерение длины линейкой).

Дифференциальный (разностный) метод заключается в измерении разности между измеряемой величиной и величиной, значение которой известно.

Схема измерения длины дифференциальным методом приведена на рисунке 7.

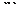1 2

1-измеряемое изделие; 2-мера длины.

Рисунок 7 – Схема измерения длины дифференциальным методом

Из схемы следует, что

x l −a , (23)

где x – длина измеряемого изделия; l – длина меры;

a – измеряемая разность длин.

Если погрешность измерения значения а не превышает некоторого значения á, то результат измерения: a±α или а(1±α/а), где α/а -относительная погрешность измерения длины a. Относительная погрешность измерения длины х:

Значение l выбирается близким к x, поэтому l>>a и α/(l-a)<<α/a. Если l=1200 мм, а=12 мм и α/а=0,01 (1 %), то

Нулевой метод заключается в сравнении измеряемой величины с величиной, значение которой заранее известно. Обе величины выбирают равными по размеру, таким образом разность между ними будет равняться нулю. Этим методом определяют массу на рычажных весах, когда масса гирь

подбирается равной измеряемой массе. Этот метод похож на дифференциальный, но в нулевом методе разность приводится к нулю.

Метод совпадений заключается в измерении по совпадающим отметкам или сигналам. Метод используется в конструкции нониуса штангенциркуля.