Классы точности средств измерений

Классом точности средств измерений называется обобщенная характеристика данного типа средств измерений, как правило, отражающая уровень их точности, выражаемая пределами допускаемых основной и дополнительных погрешностей, а также другими характеристиками, влияющими на точность.

Классы точности средств измерений проставляются на самом средстве измерений.

Рассмотрим обозначения классов точности.

1. Классы точности средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме приведенной погрешности в виде 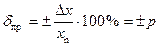(присутствует только аддитивная составляющая погрешности) или относительной погрешности 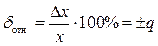(присутствует только мультипликативная составляющая погрешности), обозначаются числами p и q, которые равны пределам, выраженным в процентах.

2. Классы точности средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме относительных погрешностей (в процентах) 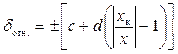(аддитивная и мультипликативная погрешности соизмеримы) обозначают числами c и d, разделяя их косой чертой, т.е. c/d.

3. Классы точности средств измерений, пределы допускаемой основной погрешности которых принято выражать в форме абсолютных погрешностей Dх= ±а обозначают буквами латинского алфавита или римскими цифрами.

4. Классы точности цифровых средств измерений со встроенными вычислительными устройствами для дополнительной обработки результатов измерений устанавливают без режима обработки.

Рассмотрим правила и примеры обозначения классов точности средств измерений, приведенные в таблице 1.

Таблица 1

Формулы для определения пределов допускаемых погрешностей	Примеры допускаемой погрешности	Обозначение класса точности	Приме-чание
В доку-мента-ции	На СИ
Dх= ±а	-	Класс точности М	М	-
Dх= ±(а+вх)	-	Класс точности С	С	-
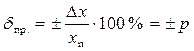
	dпр.= ±1,5	Класс точности 1,5	1,5	Если хn выражено в единицах величины
dпр.= ±0,5	Класс точности 0,5		Если хn определяется длиной шкалы или её части
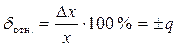
	dотн.= ±0,5	Класс точности 0,5	0,5	-
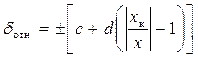
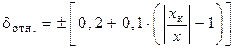
		Класс точности 0,2/0,1	0,2/ /0,1	-

При указании классов точности на средствах измерений с существенно неравномерной шкалой допускается указывать пределы допускаемой основной относительной погрешности для части шкалы, лежащей в пределах, отмеченных специальными знаками, например, точками или треугольниками.

Средствам измерений с несколькими диапазонами измерений одной и той же физической величины допускается присваивать несколько классов точности. Например, амперметру с тремя диапазонами измерения тока 0-10, 0-20 и 0-50 А могут быть присвоены различные классы точности для отдельных диапазонов.

Средствам измерений, предназначенным для измерения нескольких физических величин, допускается присваивать разные классы точности для каждой измеряемой величины. Например, средству измерений, предназначенному для измерения электрического напряжения и сопротивления, могут быть присвоены два класса точности – один как вольтметру, а другой как омметру.

ЛЕКЦИЯ 9

Структурные схемы средств измерений

В средствах измерения сигнал, несущий информацию о значении измеряемой величины, обычно претерпевает ряд преобразований с целью получения нужного выходного сигнала. Каждое преобразование сигнала можно представить себе происходящим как бы в отдельном узле, носящим название ²звено².

Соединение звеньев в определенную цепь преобразований называется структурной схемой.

Разбивка средства измерений на звенья может быть произведена по различным признакам. При анализе в статическом режиме средство измерений обычно разбивают на звенья, которые представляют собой интересующие исследователя функции преобразования.

В зависимости от соединения звеньев различают два основных вида структурных схем: прямого действия и уравновешивающего действия.

9.1. Средства измерения прямого действия

Структурная схема прибора прямого действия показана на рис. 9.1., где ИП₁, ИП₂,…,ИП_n – звенья; х, х₁, х₂,..., х_n – информатив­ные параметры сигналов.

Как видно из рис. 9.1., входной сигнал х последовательно претерпевает несколько преобразований и в итоге на выходе получается сигнал х_n .

Для измерительного прибора сигнал x_n получается в форме, доступной для непосредственного восприятия наблюдателем, на­пример, в виде отклонения указателя отсчетного устройства. Для измерительного преобразователя сигнал х_n получается в форме удобной для передачи, дальнейшего преобразования, обработки и (или) хранения.

Примером средства измерений, имеющего струк­турную схему прямого действия, может быть амперметр для измерения больших постоянных токов. В этом приборе изме­ряемый ток вначале с помощью шунта преобразуется в падение напряжения на шунте, затем в малый ток, который измеряется измерительным механизмом, т.е. преобразуется в отклонение указателя.

Структурная схема прибора прямого действия ра­зомкнутая, в ней отсутствует общая обратная связь с выхода на вход. Если все измерительные преобразователи имеют линейную функцию преобразования (х_i = k_i×х_i-1), то выходная величина связана с измеряемой величиной соотношением

х_n = k₁× k₂¼k_n× x = k× x,

где k₁ , k₂,¼, k_n – коэффициенты преобразования измери­тельных преобразователей.

Чувствительность (коэффициент преобразования) средства измерений, имеющего структурную схему прямого действия:

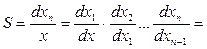k₁×k₂×k₃¼k_n .

При нелинейной функции преобразо­вания чувствительность и коэффициенты преобразования зави­сят от входного сигнала.

Мультипликативная погрешность возникает при изменении коэффициентов преобразования. С течением времени и под дей­ствием внешних факторов коэффициенты k₁, k₂, k₃ ,¼, k_nмогут изме­няться соответственно на Dk₁,Dk₂,Dk₃,¼, Dk_n.

При достаточно малых изменениях этих коэффициентов можно пренебречь членами вто­рого и большего порядков малости, тогда относительное измене­ние чувствительности

.

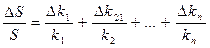Изменение чувствительности приводит к изменению выходно­го сигнала на

Dx_n= (S +DS)× x – S×x = DS× x.

Этому изменению вы­ходного сигнала соответствует абсолютная погрешность измере­ния входной величины

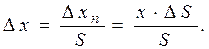
Как видно из этого выражения, погрешность, вызванная изменением чувствительности, является мультипликативной. От­носительная мультипликативная погрешность измерения

d_м = DS/S .

Аддитивная погрешность вызывается дрейфом ²нуля² звень­ев, наложением помех на полезный сигнал и т.д., приводящих к смещению графика характеристики преобразования i-гo звена на ±Dx_0i; (как показано на рис. 9.2).

Аддитивную погреш-ность можно найти, введя на структурной схеме после соответствующих звеньев дополнительные внешние сигналы Dx₀₁ , Dx₀₂, …, Dx_0n , равные смещениям характеристик преобразования звеньев.

Для оценки влияния этих дополнительных сигналов пересчи­таем (приведем) их к входу структурной схемы. Результирующее действие всех дополнительных сигналов равно действию следу­ющего дополнительного сигнала на входе:

.

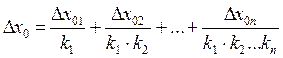Результирующая аддитивная погрешность равна Dx₀. Таким образом, в средствах измерений, имеющих структурную схему прямого действия, происхо­дит суммирование погрешностей, вносимых отдельными звень­ями, и это затрудняет изготовление средств измерений прямого действия с высокой точностью.

9.2. Средства измерений уравновешивающего действия

Структурная схема средства измерений уравновешивающего действия показана на рис. 9.4.

Структурная схема такого средства измерений содержит две цепи – цепь прямого и цепь обратного действия, т.е. в средстве измерения имеется общая отрицательная обратная связь с выхода на вход.

Для цепи обратного действия (обратной связи)

x^¢_m = x_n× b₁× b₂×…× b_m = x_n× b, (9.1)

где b – коэффициент преобразования цепи обратного действия; b₁, b₂, …, b_m - коэффициенты преобразования звеньев обратной связи.

На входе цепи прямого действия в узле СУ происходит сравнение (компенсация) входного сигнала х и выходного сигна­ла цепи обратного действия х'_m и при этом на выходе СУ получается разностный сигнал

Dх = х – х'_m .

При подаче на вход сигнала х выходной сигнал x_n, а следова­тельно, и х'_m, будут возрастать до тех пор, пока х и х'_m не станут равны. При этом по значению x_n можно судить об измеряемой величине х.

Средства измерений, имеющие такую структурную схему, могут работать как с полной, так и с неполной компенсацией.

При полной компенсации (астатическое преобразование) в установившемся режиме

Dх = х – х'_m = 0.

Это возможно в тех устройствах, у которых в цепи прямого преобразования предусмотрено интегрирующее звено с характеристикой преобразования 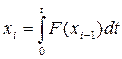. Примером такого звена является электродвигатель, для которого угол поворота вала определяется приложенным напряжением и временем.

В этом случае, получим

x_n = x/(b₁×b₂…b_m) = x/b . (9.2)

Таким образом, в момент компенсации сигнал на выходе средства измерений пропорционален входному сигналу и не за­висит от коэффициента преобразования цепи прямого действия.

Чувствительность (коэффициент преобразования)

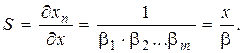
Мультипликативная относительная погрешность, обуслов­ленная нестабильностью коэффициентов преобразования звень­ев, при достаточно малых изменениях этих коэффициентов

.

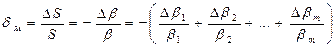Как видно из этого выражения, относительная мультиплика­тивная погрешность обусловлена только относительным измене­нием коэффициента преобразования цепи обратного действия.

Аддитивная погрешность в средствах измерений с полной компенсацией практически обусловливается порогом чувстви­тельности звеньев, расположенных до интегрирующего звена, и порогом чувствительности самого интегрирующего звена.

Под порогом чувствительности звена понимается то наимень­шее изменение входного сигнала, которое способно вызвать по­явление сигнала на выходе звена. Порог чувствительности имеют, например, электродвигатели, часто применяемые в рассматрива­емых устройствах. Для реальных звеньев график характеристики преобразования может иметь вид, как показано на рис.9.5, где ± Dх _i-1 – порог чувствительности.