Дифференциальный метод

Дифференциальный метод представляет собой метод сравнения с мерой, в котором измеряемая величина сравнивается с однородной величиной, имеющей известное значение, незначительно отличающееся от значения измеряемой величины, при котором измеряется разность между этими двумя величинами. На рис. 4.2. показана функциональная схема дифференциального метода.

Здесь мера имеет постоянное значение Х₀, разность измеряемой величины Х и меры Х₀, т.е. e = Х – Х₀, не равна ну­лю и измеряется измерительным прибором. Результат измерения на­ходится как

Y = X₀ + e .

То обстоятельство, что здесь измерительный прибор измеряет не всю величину Х, а только её часть e позволяет уменьшить влияние на результат измерения погрешности измерительного прибора, причем влияние погрешности измерительного прибора тем меньше, чем меньше разность e.

Действительно, при измерении напряжения U = 97 В вольтметром непосредственной оценки с пределом измерения 100 В и допущенной относительной погрешности измерения этого напряжения 1 % мы получаем абсолютную погрешность измерения D₁= 97 × 0,01 = 0,97 » 1 В. Если же мы будем измерять это напряжение дифференциальным методом с использованием образцового источника напряжения U₀ = 100 В, то разность напряжений U – U₀ = (97–100) В = – 3 В мы можем измерить вольтметром с пределом измерения всего 3 В. Пусть относительная погрешность измерения этого напряжения будет также равна 1 %. Это даёт абсолютную погрешность измерения напряжения 3 В, равную D₂ = 3 × 0,01 = 0,03 В. Если эту погрешность привести к измеряемому напряжению U, мы получим относительную погрешность измерения напряжения, равную D₂/U = 0,03/97 » 0,0003 (0,03 %), т.е. приблизительно в 30 раз меньше, чем при измерении напряжения U методом непосредственной оценки. Это увеличение точности измерения произошло потому, что в первом случае прибором была измерена почти вся величина с относительной погрешностью в 1 %, а во втором случае измеряется не вся величина, а только её 1/30 часть.

В этих расчетах не учитывалась погрешность меры, кото­рая полностью входит в результат измерения. Следовательно, при малых разностных величинах e точность измерения дифферен­циальным методом приближается к точности измерения нулевым ме­тодом и определяется лишь погрешностью меры. Кроме того, диф­ференциальный метод не требует меры переменной величины.

В приведенном примере измерения напряжения дифферен­циальным методом использовалось непосредственное сравнение.

Метод совпадений

Метод совпадений (или метод ²нониуса²) представляет собой метод сравнения с мерой, в котором разность между измеряемой величи­ной и величиной, воспроизводимой мерой, измеряют, используя совпадение отметок шкал или периодических сигналов.

Этот метод применяется в тех случаях, когда измеряемая величина меньше цены деления заданной меры. При этом применяются две меры с разными ценами деления, которые отлича­ются на размер оцениваемого разряда отсчетов.

Пусть имеем одну калиброванную меру с ценой деления Dx_k1 и изме­ряемую величину Dx, которая меньше цены деления. В этом случае исполь­зуют вторую меру с ценой деления Dx_k2. Таким образом, если чувствитель­ность необходимо увеличить в п раз, то соотношение между ними будет иметь вид

Dx_k2 = Dx_k1× (1 – 1/n).

В частности, при n = 10 Dx_k2 = 0,9 ×Dx_k1.

Измеряемую величину Dx устанавливают между нулевыми отметками мер и находят число N_x, равное номеру совпавших делений мер (рис. 4.3.).

В этом случае справедливо соотношение N_x× Dx_k1 = Dx + N_x× Dx_k2, откуда Dx = N_x× (Dx_k1–Dx_k2) = N_x× (Dx_k1 – 0,9 × Dx_k1) = N_x × 0,1 × Dx_k1.

Примером измерения методом совпадения может служить измерение длины детали с помощью штангенциркуля с нониусом. Другим примером может служить измерение частоты вращения детали с помощью мигающей лампы стробоскопа: наблюдая положение метки на вращающейся детали в моменты вспышек лампы, по частоте вспышек и смещению метки, определяют частоту вращения детали.

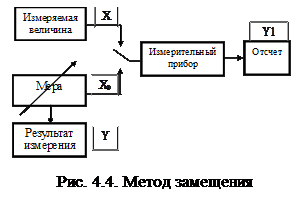
4.5. Метод замещения

Метод замещения есть метод сравнения с ме­рой, в котором измеряемую величину замещают мерой с известным значением величи­ны.

Функциональная схема метода замещения изображена на рис. 4.4.

В нем используется измерительный прибор непосредственной оцен­ки.

Техника измерения состоит в следующем. Сначала на вход из­мерительного прибора подают измеряемую величину Х и отмечают показания прибора (отсчет) Y₁. После этого вместо измеряемой величины на тот же самый вход прибора (это очень существенно) подают величину Х₀, воспроизводимую мерой. В этом случае показание прибора становится равным Y₂. Изменяя величину, воспроизводимую мерой, добиваются равенства показаний, т.е. Y₁ = Y₂. При этом можно утверждать, что Х = Х₀ независимо от погрешности измерительного прибора. Действительно, в первом случае получаем Y₁ = X + D₁, где D₁ – погрешность измерительного прибора при получении счета Y₁.

При воздействии на прибор меры

Y₂ = X + D₂.

Здесь D₂ – погрешность измерительного прибора при получении счета Y_2.

Поскольку мы добиваемся одинаковых показаний (Y₁ = Y₂), а интервал времени между двумя измерениями невелик, то на одной и той же отметке шкалы прибора погрешность одинакова, т.е. D₁ = D₂. Следовательно, из равенства Y₁ = Y₂ или X + D₁ = X + D₂ вытекает, что Х = Х_0.

Исключение погрешности измерительного прибора из результата измерений является новым достоинством метода замещения.

Таким образом, методом замещения можно осуществить точное измерение, имея прибор с большой погрешностью. Очевидно, что точность измерения методом замещения определяется погрешностью меры. Но при более строгом подходе к методу замещения следует учитывать два обстоятельства.

Во-первых, здесь сравнение разновременное, а за время между двумя измерениями погрешность измерительного прибора может несколько измениться, так что равенство D₁ = D₂ несколько нарушится. Теперь становится ясно, почему измеряемая величина и мера должны подаваться на один и тот же вход прибора. Это, прежде всего, связано с тем, что погрешность измерительного прибора на разных входах даже при одинаковых показаниях может быть разной!

Во-вторых, метод замещения сводится к получению одинаковых показаний прибора. Само равенство показаний может быть ус­тановлено с конечной точностью. А это также ведет к погрешности измерения. Точность установления равенства показаний будет больше в приборе, обладающем большей чувствительностью.

Следовательно, при измерении методом замещения можно использовать пусть не точный, но зато чувствительный и быстродействующий прибор. Тогда остаточная погрешность, обусловленная измерительным прибором, будет невелика.

Метод замещения является самым точным из всех известных методов и обычно используется для проведения наиболее точных (прецизионных) измерений.