Классификация видов измерений

Классификацию видов измерений можно проводить по различным классификационным признакам, к которым можно отнести следующее:

- способ нахождения численного значения физической величины,

- число наблюдений,

- характер зависимости измеряемой величины от времени,

- число измеряемых мгновенных значений в заданном интервале времени,

- условия, определяющие точность результатов,

- способ выражения результатов измерения.

По способунахождения численного значения физической величины измерения подразделяются на следующие виды: прямые, косвенные, совокупные и совместные.

Прямым измерением называют измерение, при котором значение измеряемой величины находят непосредственно из опытных данных. Прямые измерения выполняются при помощи средств, предназначенных для измерения данных величин. Числовое значение измеряемой величины отсчитывается непосредственно по показанию измерительного прибора. Примеры прямых измерений: измерение тока ампер­метром; напряжения – вольтметром; массы - на рычажных весах и др.

Зависимость между измеряемой величиной X и результатом измерения Y при прямом измерении характеризуется уравнением:

X = Y,

т.е. значение измеряемой величины принимается равным получен­ному результату.

К сожалению, прямое измерение не всегда можно провести. Иногда нет под рукой соответствующего измерительного прибора или он неудовлетворителен по точности, или даже вообще ещё не создан. В этом случае приходится прибегать к косвенному измере­нию.

Косвенными измерениями называют та­кие измерения, при которых значение искомой величины находят на основании известной зависимости между этой величиной и величи­нами, подвергаемыми прямым измерениям.

При косвенных измерениях измеряют не собственно определяемую величину, а другие величины, функционально с ней связанные. Значение измеряемой косвенным путем величины X находят вычислением по фор-муле

X = F(Y₁, Y₂, … ,Y_n),

где Y₁ , Y₂ , … Y_n – значения величин, полученных путем прямых измерений.

Примером косвенного измерения является определение электрического сопротивления с помощью амперметра и вольтметра. Здесь путем прямых измерений находят значения падения напряжения U на сопротивлении R и ток I через него, а искомое сопротивление R находят по формуле

R = U/I.

Операцию вычисления измеряемой величины может производить как человек, так и вычислительное устройство, помещенное в прибор.

Прямые и косвенные измерения в настоящее время широко использу­ются в практике и являются наиболее распространенными видами измерений.

Совокупные измерения – это производи­мые одновременно измерения нескольких одноименных величин, при которых искомые значения величин находят решением системы уравнений, получаемых при прямых измерениях различных сочетаний этих величин.

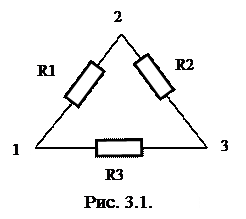
Например, для определения значений сопротивлений резисторов, соединенных треугольником (рис. 3.1), измеряют сопротивления на каждой паре вершин треугольника и получают систему уравнений:

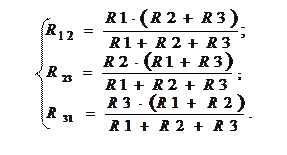Из решения этой системы уравнений получают значения сопротивлений

, , ,

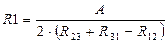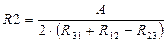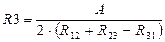где .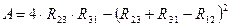

Совместные измерения – это производимые одновременно измерения двух или нескольких не одноименных величин X₁, X₂,…,X_n, значения которых находят решением системы уравнений

F_i (X₁, X₂, … ,X_n; Y_i1, Y_i2, … ,Y_im) = 0,

где i = 1, 2, …, m > n; Y_i1, Y_i2, … ,Y_im – результаты прямых или косвенных измерений; X₁, X₂, … ,X_n – значения искомых величин.

Например, индуктивность катушки

L = L₀ × (1 + w²× C× L₀),

где L₀ – индуктивность при частоте w =2× p × f стремящейся к нулю; С – межвитковая емкость. Значения L₀ и С нельзя найти прямыми или косвенными измерениями. Поэтому в простейшем случае измеряют L₁ при w₁, а затем L₂ при w₂ и составляют систему уравнений:

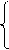L₁ = L₀× (1 + w₁²× C× L₀);

L₂ = L₀× (1 + w₂²× C× L₀),

решая которую, находят искомые значения индуктивности L₀ и емкости С

; .

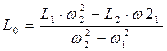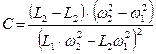Совокупные и совместные измерения – это обобщение косвен­ных измерений на случай нескольких величин.

Для повышения точности совокупных и совместных измерений обеспечивают условие m ³ n, т.е. число уравнений должно быть больше или равно числу искомых величин. Получающуюся при этом несовместную систему уравнений решают методом наименьших квадратов.

По числу наблюдений измерения подразделяются:

- на обыкновенные измерения – измерения, выполняемые с однократным наблюдением;

- статистические измерения – измерения с многократными на-блюдениями.

Наблюдение при измерении – экспериментальная операция, выполняемая в процессе измерений, в резуль­тате которой получают одно значение из группы значе­ний величин, подлежащих совместной обработке для по­лучения результатов измерений.

Результат наблюдения – результат величины, полу­чаемый при отдельном наблюдении.

По характеру зависимости измеряе­мой величины от времени измерения разделяются:

- на статические, при которых измеряемая величина оста­ется постоянной во времени в процессе измерения;

- динамические, при которых измеряемая величина изменяется в процессе измерения и является непостоянной во вре­мени.

При динамических измерениях для получения результата измерения необходимо учитывать это изменение. А для оценки точности результатов динамических измерений необходимо знание динамических свойств средств измерений.

По числу измеряемых мгновенных значений в заданном интервале времениизмерения подразделяются на дискретные и непрерывные (аналоговые).

Дискретные измерения – измерения, при которых на заданном интервале времени число измеряемых мгновенных значений конечно.

Непрерывные (аналоговые) измерения – измерения, при которых на заданном интервале времени число измеряемых мгновенных значений бесконечно.

По условиям, определяющим точность результатов, измерения бывают:

- максимально воз­можной точности, достигаемой при существующем уров­не техники;

- контрольно-поверочные, погрешность кото­рых не должна превышать некоторое заданное значение;

- технические измерения, в которых погрешность результата опреде­ляется характеристиками средств измерений.

По способу выражения результатов различают абсолютные и относительные измерения.

Абсолютные измерения – измерения, основанные на прямых измерениях одной или нескольких основных величин и (или) использовании значений физических констант.

Относительные измерения – измерения отношения величины к одноименной величине, играющей роль единицы, или измерения величины по отношению к одноименной величине, принимаемой за исходную.

Методы измерений и их классификация

Все измерения могут производиться различными методами. Различают два основных метода измерений: метод непосредственной оценки и методы сравнения c мерой.

Метод непосредственной оценки характеризуется тем, что значение измеряемой величины опреде­ляется непосредственно по отсчетному устройству измерительного прибора, заранее градуированного в единицах измеряемой величины. Этот метод является наиболее простым и поэтому широко применяется при измерении различных величин, например: измерение веса тела на пружинных весах, силы электрического тока стрелочным ампермет­ром, разности фаз цифровым фазометром и т.д.

Функциональная схема измерения методом непосредственной оценки приведена на рис. 3.2.

Мерой в приборах непосредственной оценки слу­жат деления шкалы отсчетного устройства. Они поставлены не произвольно, а на основании градуировки прибора. Таким образом, деления шкалы отсчетного устройс­тва являются как бы заменителем (²отпечатком²) значения реаль­ной физической величины и поэтому могут быть использованы не­посредственно для нахождения значений измеряемых прибором величин. Следовательно, все приборы непосредственной оценки факти­чески реализуют принцип сравнения с физическими величинами. Но это сравнение разновременное и осуществляется опосредованно, с помощью промежуточного средства – делений шкалы отсчетного устройства.

Методы сравнения с мерой – методы измерений, в которых измеряемую величину сравнивают с величиной, воспроизводимой мерой. Эти методы по сравнению с методом непосредственной оценки более точны, но немного сложнее. Группа методов сравнения с мерой включает в себя следующие методы: метод противопоставления, нулевой метод, дифференциальный метод, метод совпадения и метод замещения.

Определяющим признаком методов сравнения является то, что в процессе измерения происходит сравнение двух однородных величин – известной (воспроизводимой мерой) и измеряемой. При измерениях методами сравнения используются реальные физи­ческие меры, а не их ²отпечатки².

Сравнение может быть одновременным и разновременным. При одновременном сравнении мера и измеряемая величина воздействуют на измерительный при­бор одновременно, а при разновременном – воздействие измеряемой величины и меры на измерительный прибор раз­несено во времени. Кроме того, сравнение может быть непосредственным и опосредован­ным.

При непосредственном сравнении измеряемая величина и мера непосредст­венно воздействуют на устройство сравнения, а при опосредован­ном сравнении – через другие величины, однозначно связанные с известной и измеряемой величинами.

Одновременное сравнение осуществляется обычно методами противопоставления, нулевым, дифференциа­льным и совпадения, а разновременное - методом замещения.

ЛЕКЦИЯ 4

МЕТОДЫ ИЗМЕРЕНИЙ