Алгебраическая сумма внешних сил и сил инерции, действующих на тело в любом направлении, равна нулю».
Рассмотрим i-е звено (рис. 8.1). Пусть точка О' совпадает с центром масс этого звена. Устанавливая соответствие между рис. 11.4 и 13.1, введем следующие обозначения (все векторы заданы в базовой системе координат):
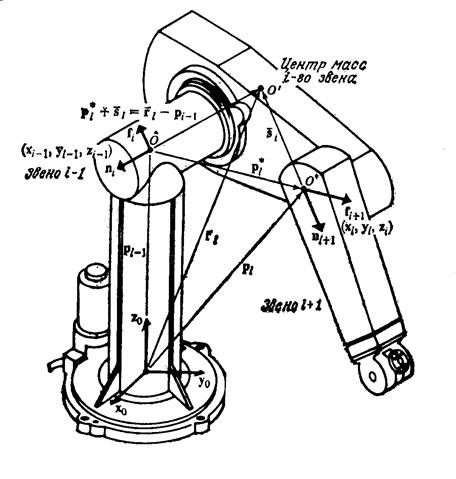
Рисунок 13.1. Силы и моменты, действующие на i-е звено
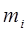 - масса i-го звена;
- масса i-го звена;
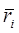 - положение центра масс i-го звена в базовой системе координат;
- положение центра масс i-го звена в базовой системе координат;
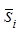 - положение центра масс i-го звена относительно начала
- положение центра масс i-го звена относительно начала
системы координат 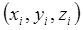 ;
;
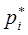 - положение начала i-й системы координат относительно
- положение начала i-й системы координат относительно
начала 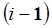 -й системы координат;
-й системы координат;
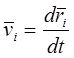 - линейная скорость центра масс i-го звена;
- линейная скорость центра масс i-го звена;
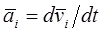 - линейное ускорение центра масс i-го звена;
- линейное ускорение центра масс i-го звена;
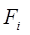 -суммарная внешняя сила, приложенная к центру масс
-суммарная внешняя сила, приложенная к центру масс
i-го звена;
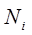 -суммарный момент внешних сил, приложенных к i-му
-суммарный момент внешних сил, приложенных к i-му
звену;
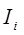 - матрица инерции i-го звена относительно его центра
- матрица инерции i-го звена относительно его центра
масс в базовой системе координат 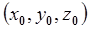 ;
;
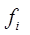 - сила, с которой
- сила, с которой 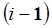 -е звено действует на i-е звено в
-е звено действует на i-е звено в
системе координат 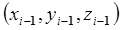 ;
;
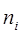 - момент, вызванный действием
- момент, вызванный действием 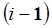 -го звена на i-е
-го звена на i-е
звено в системе координат 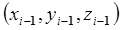 .
.
Пренебрегая силами трения в сочленениях, применив принцип Д'Аламбера к i-му звену, получаем:
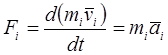 , (13-1)
, (13-1)
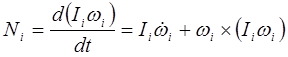 . (13-2)
. (13-2)
Входящие в эти формулы линейные скорость и ускорение центра масс i-го звена в соответствии с равенствами (12-32) и (12-35) определяются выражениями:
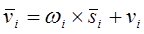 , (13-3)
, (13-3)
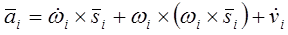 . (13-4)
. (13-4)
Суммарная сила 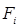 и момент
и момент 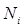 , приложенные к i-му звену, обусловлены действием на него силы тяжести, а также сил со стороны соседних
, приложенные к i-му звену, обусловлены действием на него силы тяжести, а также сил со стороны соседних 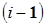 -го и
-го и 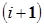 -го звеньев. Таким образом:
-го звеньев. Таким образом:
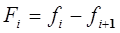 , (13-5)
, (13-5)
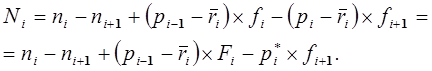 (13-6)
(13-6)
Эти уравнения можно представить в рекуррентной форме, воспользовавшись тем, что:
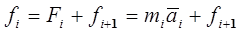 , (13-7)
, (13-7)
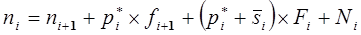 . (13-8)
. (13-8)
Полученными уравнениями, имеющими рекуррентную форму, можно воспользоваться для вычисления сил и моментов 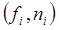
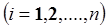 , действующих на звенья n-звенного манипулятора. Для этого достаточно учесть, что
, действующих на звенья n-звенного манипулятора. Для этого достаточно учесть, что 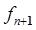 и
и 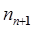 представляют собой соответственно силу и момент, с которыми объект манипулирования действует на схват манипулятора. Момент, создаваемый приводом i-го сочленения, должен быть равен сумме проекции момента
представляют собой соответственно силу и момент, с которыми объект манипулирования действует на схват манипулятора. Момент, создаваемый приводом i-го сочленения, должен быть равен сумме проекции момента 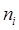 на ось
на ось 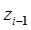 и момента вязкого трения в i-м сочленении (если сочленение – вращательное). Если же i-е сочленение – поступательное, оно реализует смещение на
и момента вязкого трения в i-м сочленении (если сочленение – вращательное). Если же i-е сочленение – поступательное, оно реализует смещение на 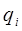 единиц длины относительно системы координат
единиц длины относительно системы координат 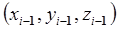 вдоль оси
вдоль оси 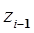 . В этом случае сила
. В этом случае сила 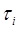 , создаваемая в этом сочленении, должна быть равна в системе координат
, создаваемая в этом сочленении, должна быть равна в системе координат 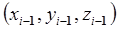 сумме проекции силы
сумме проекции силы 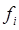 на ось
на ось 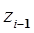 и силы вязкого трения. Таким образом, момент (сила)
и силы вязкого трения. Таким образом, момент (сила) 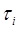 , создаваемый приводом i-го сочленения, определяется формулой:
, создаваемый приводом i-го сочленения, определяется формулой:
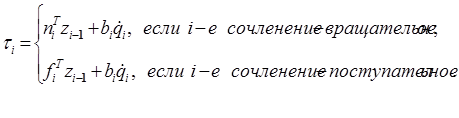 , (13-9)
, (13-9)
где 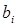 - коэффициент вязкого трения в i-м сочленении.
- коэффициент вязкого трения в i-м сочленении.
Если основание манипулятора закреплено на платформе и 0-е звено неподвижно, то 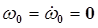 ,
, 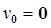 , и с учетом силы тяжести:
, и с учетом силы тяжести:
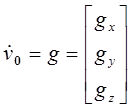 , где
, где 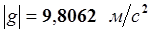 . (13-10)
. (13-10)
Таким образом, для исследователя существует возможность выбора одной из трех следующих форм представления уравнений движения манипулятора:
1. удобная для анализа, но неэффективная в вычислительном плане форма Лагранжа-Эйлера;
2. эффективная с вычислительной точки зрения, но малопригодной для анализа форма Ньютона-Эйлера;
3. достаточно удобные для анализа при умеренных вычислительных затратах обобщенные уравнения Д'Аламбера.
Лекция 14
Планирование траекторий манипулятора
Планирование траекторий движения манипулятора – это задача выбора закона управления, обеспечивающего движение манипулятора вдоль некоторой заданной траектории. Перед началом движения манипулятора важно знать:
1. существуют ли на его пути какие-либо препятствия;
2. накладываются ли какие-либо ограничения на траекторию схвата.
В зависимости от ответов на эти вопросы выбирается один из четырех типов управления манипулятором (табл. 14.1).
Таблица 14.1. Типы управления манипулятором
| Препятствия на пути манипулятора | |||
| Присутствуют | Отсутствуют | ||
| Ограничения на траекторию манипулятора | Присутствуют | I.Автономное планирование траектории, обеспечиваю-щее обход препятствий, плюс регулирование дви-жения вдоль выбранной траектории в процессе работы манипулятора | II.Автономное плани-рование траектории плюс регулирование движения вдоль выб-ранной траектории в процессе работы манипулятора |
| Отсутствуют | III.Позиционное управление плюс обнаружение и обход препятствий в процессе движения | IV.Позиционное управление |
Рассмотрим планирование траектории манипулятора при отсутствии препятствий (II и IV тип). Задача состоит в разработке математического аппарата для выбора и описания желаемого движения манипулятора между начальной и конечной точками траектории.
При планировании траекторий обычно применяется один из двух подходов:
1. Задается точный набор ограничений (например, непрерывность и гладкость) на положение, скорость и ускорение обобщенных координат манипулятора в некоторых (называемых узловыми) точках траектории. Планировщик траекторий после этого выбирает из некоторого класса функций (как правило, среди многочленов, степень которых не превышает некоторое заданное n) функцию, проходящую через узловые точки и удовлетворяющую в них заданным ограничениям. Определение ограничений и планирование траектории производится в присоединенных координатах.
2. Задается желаемая траектория манипулятора в виде некоторой аналитически описываемой функции, как, например, прямолинейную траекторию в декартовых координатах. Планировщик производит аппроксимацию заданной траектории в присоединенных или декартовых координатах.
Планирование в присоединенных переменных обладает тремя преимуществами:
1) задается поведение переменных, непосредственно управляемых в процессе движения манипулятора;
2) планирование траектории может осуществляться в реальном времени;
3) траектории в присоединенных переменных легче планировать.
4) Должны быть сведены к минимуму бесполезные движения типа «блуждания».
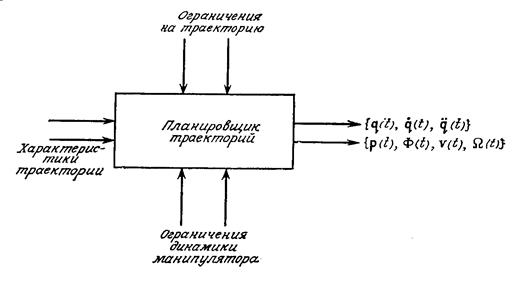
Рисунок 14.1. Блок-схема планировщика траекторий
Недостаток – сложность определения положения звеньев и схвата в процессе движения. Это необходимо для предотвращения столкновения с препятствием.
В общем случае основной алгоритм формирования узловых точек траектории в пространстве присоединенных переменных весьма прост:
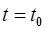 ;
;
цикл: ждать следующего момента коррекции;
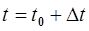 ;
;
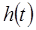 =заданное положение манипулятора в пространстве присоединенных переменных
=заданное положение манипулятора в пространстве присоединенных переменных
в момент времени 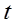 ;
;
Если 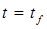 , выйти из процедуры;
, выйти из процедуры;
Выполнить цикл.
Здесь 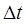 – интервал времени между двумя последовательными моментами коррекции параметров движения манипулятора.
– интервал времени между двумя последовательными моментами коррекции параметров движения манипулятора.
Из алгоритма видно, что все вычисления производятся для определения траекторной функции 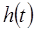 , которая должна обновляться в каждой точке коррекции параметров движения манипулятора.
, которая должна обновляться в каждой точке коррекции параметров движения манипулятора.
На планируемую траекторию накладывается четыре ограничения:
1) Узловые точки должны легко вычисляться нерекуррентным способом.
2) Промежуточные положения должны определяться однозначно.
3) Должна быть обеспечена непрерывность присоединенных координат и их двух первых производных, чтобы планируемая траектория в пространстве присоединенных переменных была гладкой.
4)
Перечисленным ограничениям удовлетворяют траектории, описываемые последовательностями полиномов.
В общем случае планирование траекторий в декартовых координатах состоит из двух последовательных шагов:
1) формирование последовательности узловых точек в декартовом пространстве, расположенных вдоль планируемой траектории схвата;
2) выбор некоторого класса функций, аппроксимирующих участки траектории между узловыми точками в соответствии с некоторым критерием (например, прямые, дуги круга, параболы и т.п.).
Первый подход позволяет обеспечить высокую точность движения вдоль заданной траектории. Однако, при отсутствии датчиков положения схвата в декартовых координатах, для перевода декартовых координат в присоединенные требуется большое количество вычислений, что замедляет время движения манипулятора. Поэтому используется второй подход – декартовы координаты узловых точек преобразуются в соответствующие присоединенные координаты с последующим проведением интерполяции в пространстве присоединенных переменных полиномами низкой степени. Это сокращает вычисления и позволяет учесть ограничения динамики манипулятора. Но точность движения снижается.
Дата добавления: 2016-05-25; просмотров: 1707;
