В любом графе число вершин нечетной степени всегда четно.
Лемма о рукопожатиях. Число вершин в графе (или мультиграфе без петель), имеющих нечетную степень, четно.
Доказательство леммы. Заметим, что сумма степеней всех вершин в графе (или мультиграфе без петель) должна быть четной. Это следует из того, что если взять вершины, вообще не связанные друг с другом, то сумма степеней этих вершин равна нулю. Прибавляя любое ребро, которое связывает две вершины, увеличиваем сумму всех степеней на 2 единицы. Таким образом, сумма всех степеней вершин четна. Удаляя из этой суммы степени четных вершин, получим, что сумма степеней нечетных вершин, должна быть четной. Это значит, что само число таких вершин должно быть четным. Лемма доказана.
Изоморфизм графов
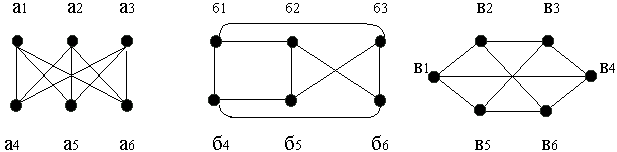
Графы на рис. 1.3 все выглядят как различные, но каждый из них можно перерисовать так, чтобы он стал (если не обращать внимание на обозначение вершин) идентичен другому. То есть все эти графы в некотором смысле «эквивалентны», имеют одинаковую структуру. Определим более точно характер этой «эквивалентности».
| (а) (б) (в) Рис. 1.3. Изоморфные графы |
Графы G=(X,U) и G'=(X',U') изоморфны (пишут G@G'), если существует взаимно-однозначное соответствие между множествами X и X', сохраняющее смежность вершин (т.е. такое соответствие, при котором вершины xi и xj из множества X смежны тогда и только тогда, когда смежны соответствующие им вершины x'i и x'j из множества X').
Изоморфизм графа рис. 1.3 (а), к графу рис.1.3 (б) обнаруживается, если задать следующее соответствие между вершинами:
| а1-б1, а2-б5, а3-б6, а4-б3, а5-б2, а6-б4 | (1.1) |
Посмотрим, как это делается.
Для рис. 1.3(а) перечень неповторяющихся ребер:
| (а1,а4) (а1,а5) (а1,а6) (а2,а4) (а2,а5) (а2,а6) (а3,а4) (а3,а5) (а3,а6) | (1.2) |
Для рис. 1.3(б) перечень неповторяющихся ребер:
| (б1,б3) (б1,б2) (б1,б4) (б5,б3) (б5,б2) (б5,б4) (б6,б3) (б6,б2) (б6,б4) | (1.3) |
Если к (1.2) применить выражение (1.1), то получится выражение (1.3), т.е. графы на рис. 1.3 (а) и рис. 1.3(б) изоморфны.
Установить изоморфизм графа рис. 1.3(в), к графам на рис. 1.3 (а) и рис. 1.3(б) предлагается самостоятельно, определив надлежащее соответствие между их вершинами.
Для рис. 1.3(в) перечень неповторяющихся ребер:
| (в1,в2) (в1,в4) (в1,в5) (в3,в2) (в3,в4) (в3,в5) (в6,в2) (в6,в4) (в6,в5) | (1.4) |
При сопоставлении выражений (1.2) и (1.4), получается выражение (1.5) устанавливающее изоморфизм графа на рис. 1.3(в), к графу на рис. 1.3 (а):
| а1-в1, а2-в3, а3-в6, а4-в2, а5-в4, а6-в5 | (1.5) |
При сопоставлении выражений (1.3) и (1.4), получается выражение (1.6) устанавливающее изоморфизм графа на рис. 1.3(в), к графу на рис. 1.3 (а):
| б1-в1, б2-в4, б3-в2, б4-в5, б5-в3, б6-в6 | (1.6) |
Дата добавления: 2016-05-16; просмотров: 11956;
