Абсолютная и условная сходимость числового ряда
Определение. Числовой ряд называется знакопеременным, если среди его членов встречаются как положительные, так и отрицательные.
Если дан знакопеременный числовой ряд 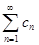 , то всегда можно рассмотреть положительный ряд
, то всегда можно рассмотреть положительный ряд 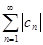 , составленный из модулей членов исходного ряда.
, составленный из модулей членов исходного ряда.
Теорема 4.1.Если сходится ряд из модулей 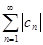 , то сходится и сам ряд
, то сходится и сам ряд 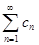 .
.
Доказательство.Предположим, что числовой ряд 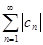 сходится. Положим
сходится. Положим
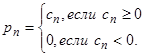
Тогда для любого номера n выполняется неравенство 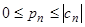 . Положительный ряд
. Положительный ряд 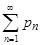 сходится, так как имеет сходящуюся мажоранту
сходится, так как имеет сходящуюся мажоранту 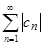 . Положим
. Положим
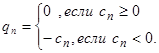
Заметим, что 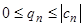 , n
, n 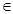 N. Следовательно, ряд
N. Следовательно, ряд 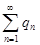 сходится, так как имеет сходящуюся мажоранту
сходится, так как имеет сходящуюся мажоранту 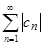 . Так как числовые ряды
. Так как числовые ряды 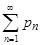 и
и 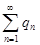 сходятся, то сходится и ряд
сходятся, то сходится и ряд 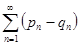 . С другой стороны,
. С другой стороны,
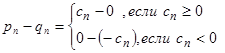 .
.
Значит, pn − qn = cn , где n  N. Тогда исходный числовой ряд
N. Тогда исходный числовой ряд 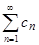 сходится.
сходится.
Определение. Говорят, что числовой ряд 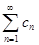 сходится абсолютно, если сходится ряд, составленный из модулей членов этого ряда
сходится абсолютно, если сходится ряд, составленный из модулей членов этого ряда 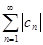 .
.
Если числовой ряд 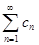 сходится, а ряд из модулей его членов
сходится, а ряд из модулей его членов 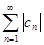 расходится, то ряд
расходится, то ряд 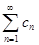 называется сходящимся условно.
называется сходящимся условно.
Чтобы привести пример ряда, сходящегося условно, рассмотрим знакочередующиеся ряды.
Определение. Числовой ряд называется знакочередующимся, если каждый последующий член этого ряда отличается знаком от предыдущего.
Можно считать, что знакочередующийся числовой ряд имеет следующий вид:
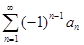 , где an > 0.
, где an > 0.
Заметим, что первый член ряда положителен.
Теорема 4.2(теорема Лейбница). Знакочередующийся числовой ряд 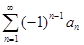 , an > 0, сходится, если последовательность {an} монотонно стремится к нулю, то есть выполняются условия:
, an > 0, сходится, если последовательность {an} монотонно стремится к нулю, то есть выполняются условия:
1) 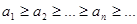 и 2)
и 2) 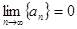 .
.
Доказательство.Рассмотрим частичные суммы данного ряда с четными номерами. Тогда
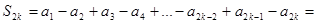
= 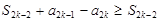 , где k
, где k  N.
N.
Это означает, что последовательность 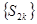 является неубывающей. Кроме того,
является неубывающей. Кроме того,
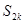 = a1 − (a2 − a3) − (a4 − a5) −…−
= a1 − (a2 − a3) − (a4 − a5) −…− 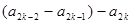 ≤ a1, k
≤ a1, k  N.
N.
Так как неубывающая последовательность 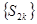 ограничена сверху, то она сходится. Пусть
ограничена сверху, то она сходится. Пусть 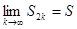 . С другой стороны,
. С другой стороны,
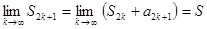 .
.
Таким образом, последовательность частичных сумм данного знакочередующегося ряда является объединением двух подпоследовательностей, сходящихся к одному и тому же числу. Значит, сходится и сама последовательность всех частичных сумм ряда. Теорема доказана.
Следствие 1.Числовой ряд 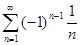 сходится условно. Действительно, данный ряд является знакочередующимся, причем 1>
сходится условно. Действительно, данный ряд является знакочередующимся, причем 1> 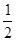 >
> 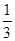 >…>
>…> 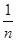 >…, a
>…, a 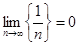 . По теореме Лейбница этот ряд сходится. Однако ряд, составленный из модулей его членов
. По теореме Лейбница этот ряд сходится. Однако ряд, составленный из модулей его членов 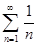 , является гармоническим числовым рядом, который расходится. Значит, ряд
, является гармоническим числовым рядом, который расходится. Значит, ряд 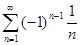 сходится лишь условно.
сходится лишь условно.
Следствие 2. Если знакочередующийся числовой ряд 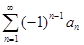 , an > 0, удовлетворяет всем условиям теоремы Лейбница, то имеет место неравенство
, an > 0, удовлетворяет всем условиям теоремы Лейбница, то имеет место неравенство
|S − Sn| ≤ an + 1, n  N.
N.
Доказательство. Последовательность 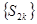 является неубывающей, а
является неубывающей, а 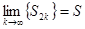 . Отсюда следует, что
. Отсюда следует, что 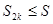 , k
, k  N. С другой стороны, последовательность
N. С другой стороны, последовательность 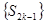 является невозрастающей. Действительно,
является невозрастающей. Действительно,
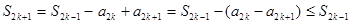 , k
, k  N.
N.
Так как 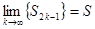 , то S2k −1 ≥ S, k
, то S2k −1 ≥ S, k  N.
N.
Если n − число четное, то 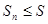 ,
, 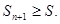 Это значит, что
Это значит, что 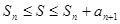 . Отсюда
. Отсюда
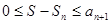 .
.
Если n − нечётное число, то 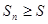 ,
, 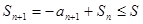 . Тогда
. Тогда 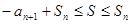 . Отсюда
. Отсюда
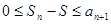 .
.
Таким образом, 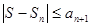 , n
, n  N. Следствие доказано.
N. Следствие доказано.
Пример. Знакочередующийся числовой ряд 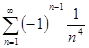 удовлетворяет всем условиям теоремы Лейбница. Чтобы найти сумму этого ряда с точностью до 0,01, выясним для какого наименьшего n выполняется неравенство an + 1 =
удовлетворяет всем условиям теоремы Лейбница. Чтобы найти сумму этого ряда с точностью до 0,01, выясним для какого наименьшего n выполняется неравенство an + 1 = 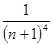 < 0,01. Так как (n +1)4 >100, то n = 3. Тогда
< 0,01. Так как (n +1)4 >100, то n = 3. Тогда 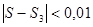 . Значит
. Значит
S 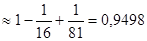
с точностью до 0,01.
Задачи.
4.1. Исследовать на сходимость знакопеременный ряд:
а) 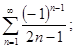 б)
б) 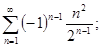 в)
в) 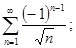 г)
г) 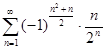 ;
;
д) 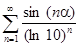 ; е)
; е) 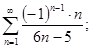
ж) 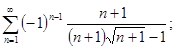 з)
з) 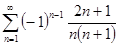 .
.
4.2. Исследовать на сходимость числовой ряд:
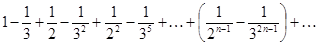
4.3. Доказать сходимость ряда и найти его сумму
с точностью до 0,01:
а) 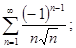 б)
б) 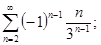 в)
в) 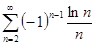 .
.
Дата добавления: 2016-07-09; просмотров: 3929;
