Простейшие свойства сходящихся числовых рядов
1. Если сходятся числовые ряды  и
и 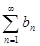 , а λ и μ − некоторые числа, то сходится и числовой ряд
, а λ и μ − некоторые числа, то сходится и числовой ряд 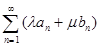 .
.
Доказательство.Так как сходятся числовые ряды  и
и 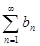 , то сходятся последовательности частичных сумм этих рядов. Пусть
, то сходятся последовательности частичных сумм этих рядов. Пусть 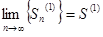 ,
, 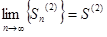 . Очевидно, что
. Очевидно, что
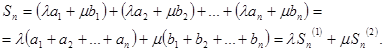
Тогда
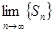 =
= 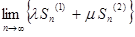 =
= 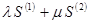 .
.
Следовательно, ряд 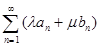 сходится, так как сходится последовательность его частичных сумм.
сходится, так как сходится последовательность его частичных сумм.
Замечание.Если 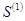 и
и 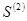 − суммы числовых рядов
− суммы числовых рядов  и
и 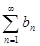 соответственно, то число
соответственно, то число 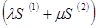 является суммой числового ряда
является суммой числового ряда 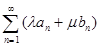 .
.
Определение. Числовой ряд 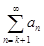 называется остатком числового ряда
называется остатком числового ряда  .
.
Например, числовой ряд 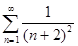 является остатком ряда
является остатком ряда 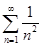 . Действительно,
. Действительно,
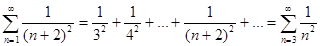 .
.
2. Если сходится числовой ряд  , то сходится и любой остаток этого ряда.
, то сходится и любой остаток этого ряда.
Доказательство.Так как ряд  сходится, то существует предел
сходится, то существует предел 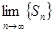 = S. Рассмотрим остаток этого ряда
= S. Рассмотрим остаток этого ряда 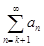 . Тогда последовательность частичных сумм остатка имеет вид:
. Тогда последовательность частичных сумм остатка имеет вид:
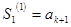 ,
, 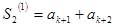 , ... ,
, ... , 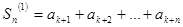 ,.. .
,.. .
Очевидно, что 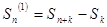 . Тогда
. Тогда
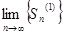 =
= 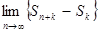 =
= 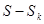 .
.
Это означает, что остаток 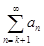 сходится.
сходится.
3. Если сходится некоторый остаток числового ряда  , то сходится и сам ряд.
, то сходится и сам ряд.
Доказательство. Предположим, что сходится остаток 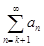 . Это означает, что последовательность частичных сумм остатка
. Это означает, что последовательность частичных сумм остатка
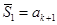 ,
, 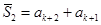 ,...,
,..., 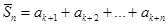 ,...
,...
сходится к числу 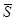 . Так как
. Так как 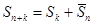 , а последовательность
, а последовательность 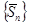 сходится, то сходится и последовательность
сходится, то сходится и последовательность 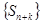 . Значит, сходится и последовательность частичных сумм
. Значит, сходится и последовательность частичных сумм 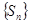 самого ряда
самого ряда  , так как лишь конечное число её членов не входит в сходящуюся подпоследовательность
, так как лишь конечное число её членов не входит в сходящуюся подпоследовательность 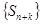 .
.
Задачи.
2.1. Найти сумму числового ряда  , если:
, если:
а) a n = 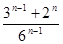 , n
, n  N;
N;
б) a n = 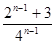 , n
, n  N;
N;
в) a n = 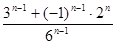 , n
, n  N.
N.
2.2. Доказать, что ряд 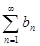 является остатком числового ряда
является остатком числового ряда  , если:
, если:
а) bn = 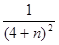 ; a n =
; a n = 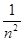 , n
, n  N;
N;
б) bn = 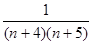 ; a n =
; a n = 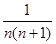 , n
, n  N;
N;
в) bn = 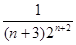 ; a n =
; a n = 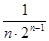 , n
, n  N.
N.
2.3. Доказать, что числовой ряд ( 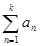 +
+ 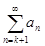 ) сходится тогда и только тогда, когда сходится ряд (
) сходится тогда и только тогда, когда сходится ряд ( 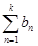 +
+ 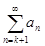 ).
).
Дата добавления: 2016-07-09; просмотров: 1646;
