Понятие сходимости и суммы числового ряда
Пусть дана числовая последовательность
a1, a 2 ,..., a n , ...
Определение.Выражение вида
a 1 + a 2 +...+ a n +... (1.1)
называется числовым рядом. Числа a1, a 2,..., a n, ... – это члены числового ряда. Число an называется общим членом числового ряда. Числовой ряд (1.1)удобно записывать кратко с помощью символа суммирования  . Например
. Например
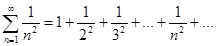
Если дан числовой ряд  , то всегда можно рассмотреть последовательность его частичных сумм
, то всегда можно рассмотреть последовательность его частичных сумм 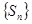 , где
, где
S1 = a 1 ,
S2 = a 1+ a 2 ,
S3 = a 1+ a 2 + a 3 ,
…
Sn = a 1+ a 2 +...+ a n ,
…
Примеры.1.Числовой ряд 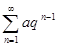 , a ≠ 0, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии. Если q ≠ 1, то
, a ≠ 0, называют геометрической прогрессией, а число q – знаменателем геометрической прогрессии. Если q ≠ 1, то
S1 = a,
S2= a + a q = a 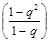 ,
,
S3 = a + a q + a q2= a 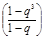 ,
,
….
Sn = a + aq + aq 2 + ...+ aq n − 1= a 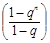 ,
,
…
2. Дан числовой ряд 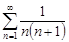 . Найдем последовательность его частичных сумм:
. Найдем последовательность его частичных сумм:
S1 = 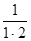 = 1−
= 1− 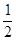 ;
;
S2 = S1 + 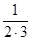 = 1−
= 1− 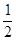 +
+ 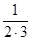 = 1−
= 1− 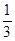 ;
;
S3 = S2 + 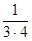 = 1−
= 1− 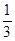 +
+ 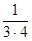 =1−
=1− 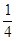 ;
;
...
Sn = Sn−1 + 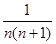 = 1−
= 1− 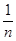 +
+ 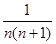 = 1 −
= 1 − 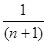 ;
;
…
Основное определение.Числовой ряд 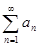 называется сходящимся, если сходится последовательность его частичных сумм
называется сходящимся, если сходится последовательность его частичных сумм 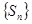 .
.
Числовой ряд 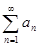 называется расходящимся, если последовательность его частичных сумм
называется расходящимся, если последовательность его частичных сумм 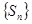 является расходящейся.
является расходящейся.
Если числовой ряд  сходится, то существует конечный предел
сходится, то существует конечный предел 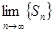 . Значение предела называется суммой числового ряда
. Значение предела называется суммой числового ряда  и обозначается через S. Таким образом, согласно определению
и обозначается через S. Таким образом, согласно определению
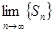 = S.
= S.
Примеры.1.Геометрическая прогрессия 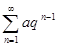 , a ≠ 0, сходится при | q| < 1и имеет сумму
, a ≠ 0, сходится при | q| < 1и имеет сумму 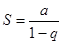 .
.
Доказательство.Так как Sn = a 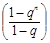 , то
, то
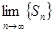 =
= 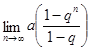 =
= 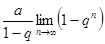 =
= 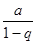 = S,
= S,
поскольку 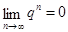 при | q| < 1.
при | q| < 1.
2. Числовой ряд 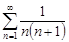 сходится и имеет сумму S = 1. Действительно,
сходится и имеет сумму S = 1. Действительно,
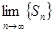 =
= 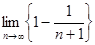 = 1.
= 1.
3. Числовой ряд 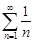 называется гармоническим рядом . Покажем, что гармонический ряд расходится. Рассмотрим частичные суммы
называется гармоническим рядом . Покажем, что гармонический ряд расходится. Рассмотрим частичные суммы 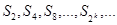 гармонического ряда:
гармонического ряда:
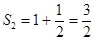 ,
,
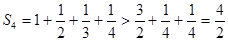 ,
,
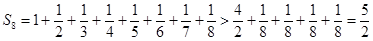 ,
,
...
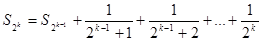 >
>
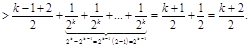
…
Отсюда следует, что последовательность 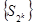 является неограниченной. Тогда сама последовательность частичных сумм
является неограниченной. Тогда сама последовательность частичных сумм 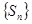 гармонического ряда расходится, так как имеет расходящуюся подпоследовательность. Значит, гармонический ряд расходится.
гармонического ряда расходится, так как имеет расходящуюся подпоследовательность. Значит, гармонический ряд расходится.
Основной задачей в теории числовых рядов является выяснение каким является числовой ряд − сходящимся или расходящимся. Поэтому важную роль играют различные признаки сходимости.
Теорема 1.1(необходимый признак сходимости). Если числовой ряд  сходится, то предел его общего члена равен нулю, то есть
сходится, то предел его общего члена равен нулю, то есть 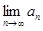 = 0.
= 0.
Доказательство.Предположим, что числовой ряд  сходится. Это означает, что сходится последовательность его частичных сумм
сходится. Это означает, что сходится последовательность его частичных сумм 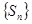 . Пусть
. Пусть 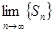 = S. Тогда последовательность
= S. Тогда последовательность 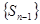 также сходится к S. Очевидно, что
также сходится к S. Очевидно, что
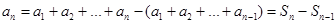 .
.
Тогда 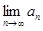 =
= 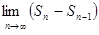 =
= 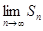 −
− 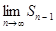 = S − S = 0.
= S − S = 0.
Замечание. Приведенный признак сходимости является необходимым, но недостаточным. Например, гармонический ряд 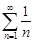 расходится. Однако
расходится. Однако 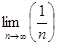 = 0.
= 0.
С помощью необходимого признака удобно устанавливать расходимость числовых рядов, так как имеет место следующее следствие теоремы 1.1.
Следствие.Если общий член ряда  не стремится к нулю, то есть предел
не стремится к нулю, то есть предел 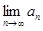 ≠ 0 или не существует, то числовой ряд
≠ 0 или не существует, то числовой ряд  расходится.
расходится.
Примеры.1.Числовой ряд 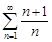 расходится, поскольку
расходится, поскольку
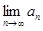 =
= 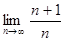 =
= 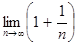 = 1 ≠ 0.
= 1 ≠ 0.
2. Геометрическая прогрессия 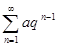 , a ≠ 0, расходится при
, a ≠ 0, расходится при 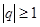 . Действительно, если q = 1, то геометрическая прогрессия имеет вид:
. Действительно, если q = 1, то геометрическая прогрессия имеет вид:
a + a +...+ a +... .
Тогда 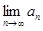 = a ≠ 0.
= a ≠ 0.
Если q = −1, то геометрическая прогрессия имеет вид:
a − a + a − a +... .
Тогда предел общего члена ряда 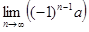 не существует.
не существует.
Если же 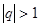 , то последовательность
, то последовательность 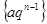 является неограниченной. Таким образом, во всех рассмотренных случаях геометрическая прогрессия расходится по необходимому признаку сходимости.
является неограниченной. Таким образом, во всех рассмотренных случаях геометрическая прогрессия расходится по необходимому признаку сходимости.
Задачи.
1.1. Для числового ряда 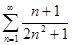 найти частичные суммы
найти частичные суммы
S2, S4, S5, S7.
1.2. Построить последовательность частичных сумм 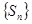 числового ряда
числового ряда  и найти сумму ряда, если:
и найти сумму ряда, если:
а) a n = 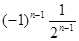 , n
, n  N;
N;
б) a n = 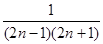 , n
, n  N;
N;
в) a n = 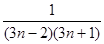 , n
, n  N;
N;
г) a n = 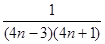 , n
, n  N;
N;
д) a n = 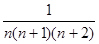 , n
, n  N;
N;
е) a n = 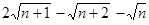 , n
, n  N.
N.
Замечание. Запись n  N, где N − множество всех натуральных чисел, означает, что n = 1,2,3,.. .
N, где N − множество всех натуральных чисел, означает, что n = 1,2,3,.. .
1.3. Построить последовательность частичных сумм 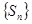 числового ряда
числового ряда  и найти сумму ряда, если:
и найти сумму ряда, если:
а) a n = 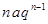 , │q│< 1, n
, │q│< 1, n  N;
N;
б) a n = 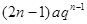 , │q│< 1, n
, │q│< 1, n  N;
N;
в) a n = 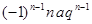 , │q│< 1, n
, │q│< 1, n  N;
N;
г) a n = 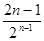 , n
, n  N;
N;
д) a n = 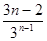 , n
, n  N.
N.
1.4. С помощью необходимого признака сходимости числового ряда доказать расходимость ряда:
а) 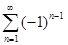 ; б)
; б) 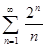 ;
;
в) 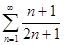 ; г)
; г) 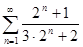 ;
;
д) 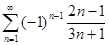 ; е)
; е) 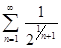 ;
;
ж) 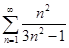 ; з)
; з) 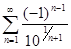 .
.
Дата добавления: 2016-07-09; просмотров: 1185;
