Свойства абсолютно и условно сходящихся числовых рядов
Как известно из арифметики, от перемены мест слагаемых сумма не изменяется. Вопрос: можно ли распространить это правило на числовые ряды?
Определение. Говорят, что числовой ряд 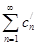 получен из ряда
получен из ряда 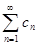 перестановкой его членов, если
перестановкой его членов, если
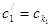 ,
, 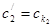 , …,
, …,  , … ,
, … ,
где 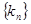 − последовательность натуральных чисел, в которой каждое натуральное число встречается один и только один раз.
− последовательность натуральных чисел, в которой каждое натуральное число встречается один и только один раз.
Например, числовой ряд
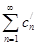 , где
, где 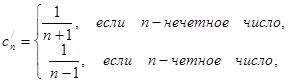
получен из гармонического ряда 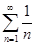 перестановкой его членов.
перестановкой его членов.
Лемма 1. Любая перестановка членов положительного ряда не изменяет его сходимости и не меняет сумму.
Доказательство. Предположим, что положительный числовой ряд 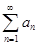 сходится, а его сумма равна S. Из сходимости ряда
сходится, а его сумма равна S. Из сходимости ряда 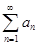 следует, что последовательность его частичных сумм ограничена сверху, т.е.
следует, что последовательность его частичных сумм ограничена сверху, т.е. 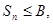 n
n  N. Если ряд
N. Если ряд 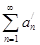 получен из исходного ряда
получен из исходного ряда 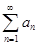 перестановкой его членов, то
перестановкой его членов, то 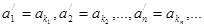 . Следовательно,
. Следовательно,
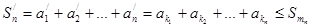 , (6.1)
, (6.1)
где 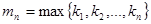 . Тогда
. Тогда 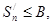 n
n  N. Значит, последовательность частичных сумм ряда
N. Значит, последовательность частичных сумм ряда 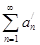 ограничена сверху. По теореме 3.1 положительный ряд
ограничена сверху. По теореме 3.1 положительный ряд 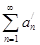 сходится. В неравенстве (6.1) можно перейти к пределу при
сходится. В неравенстве (6.1) можно перейти к пределу при 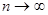 . Тогда получим
. Тогда получим
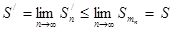 . (6.2)
. (6.2)
Таким образом, при перестановке членов положительного ряда сумма ряда не увеличивается.
Очевидно, что исходный числовой ряд 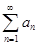 можно получить
можно получить
перестановкой членов ряда 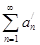 . Тогда
. Тогда
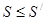 . (6.3).
. (6.3).
Из неравенств (6.2) и (6.3) следует, что  .
.
Лемма 2.Дан знакопеременный числовой ряд 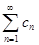 . Пусть
. Пусть
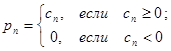 ,
, 
Тогда справедливы следующие утверждения:
- числовой ряд
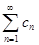 сходится абсолютно тогда и только тогда, когда положительные ряды
сходится абсолютно тогда и только тогда, когда положительные ряды 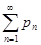 и
и 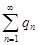 оба сходятся;
оба сходятся; - если числовой ряд
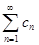 сходится условно, то положительные ряды
сходится условно, то положительные ряды 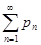 и
и 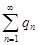 оба расходятся.
оба расходятся.
Доказательство. Предположим, что числовой ряд 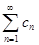 сходится абсолютно. Это означает, что сходится ряд
сходится абсолютно. Это означает, что сходится ряд 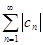 . Положительные ряды
. Положительные ряды 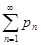 и
и 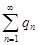 оба сходятся, так как
оба сходятся, так как 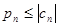 и
и 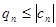 , n
, n  N. Если же сходятся положительные ряды
N. Если же сходятся положительные ряды 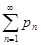 и
и 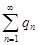 , то сходится и ряд
, то сходится и ряд 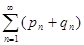 . Значит, будет сходиться и ряд
. Значит, будет сходиться и ряд 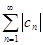 , так как
, так как 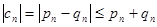 , n
, n  N.
N.
Для доказательства второго утверждения предположим, что сходится ряд 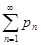 . Тогда будет сходиться и ряд
. Тогда будет сходиться и ряд 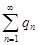 , так как
, так как 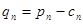 , n
, n  N. Тогда из первого утверждения следует, что ряд
N. Тогда из первого утверждения следует, что ряд 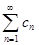 сходится абсолютно, что противоречит условию. Значит, ряд
сходится абсолютно, что противоречит условию. Значит, ряд 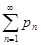 является расходящимся. Аналогично устанавливается расходимость ряда
является расходящимся. Аналогично устанавливается расходимость ряда 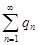 .
.
Теорема 6.1. Любая перестановка членов абсолютно сходящегося числового ряда не изменяет его сходимости и не меняет сумму.
Доказательство. Предположим, что числовой ряд 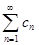 сходится абсолютно. Положим
сходится абсолютно. Положим
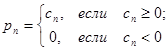 ,
, 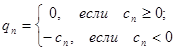 .
.
По лемме 2 положительные ряды 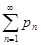 и
и 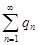 оба сходятся. Тогда сумма S исходного ряда равна:
оба сходятся. Тогда сумма S исходного ряда равна: 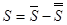 , где
, где 
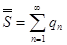 . Рассмотрим числовой ряд
. Рассмотрим числовой ряд 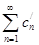 , полученный перестановкой членов исходного ряда
, полученный перестановкой членов исходного ряда 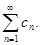 Положим
Положим
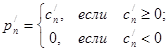 ,
, 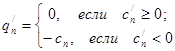 .
.
Очевидно, что ряд 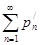 получен из ряда
получен из ряда 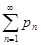 перестановкой его членов, а ряд
перестановкой его членов, а ряд 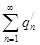 получен перестановкой членов ряда
получен перестановкой членов ряда 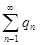 . По лемме 1 ряды
. По лемме 1 ряды 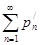 и
и 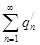 оба сходятся, причём
оба сходятся, причём  ,
, 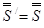 . По лемме 2 ряд
. По лемме 2 ряд 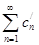 сходится, причем
сходится, причем
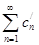 =
= 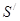 =
= 
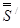 =
= 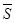 −
− 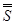 = S =
= S = 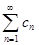 .
.
Теорема 6.2 (теорема Римана). Предположим, что числовой ряд 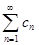 сходится условно. Тогда справедливы следующие утверждения:
сходится условно. Тогда справедливы следующие утверждения:
- Члены ряда
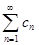 можно переставить так, что полученный ряд будет расходиться.
можно переставить так, что полученный ряд будет расходиться. - Каково бы ни было число Q, члены ряда
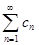 можно переставить так, что сумма полученного ряда будет равна Q.
можно переставить так, что сумма полученного ряда будет равна Q.
Доказательство. Докажем первое утверждение. Положим:
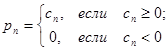 ,
,  .
.
По лемме 2 положительные ряды 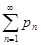 и
и 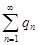 оба расходятся. Это означает, что последовательности частичных сумм обоих рядов неограничены сверху. Будем выписывать по порядку неотрицательные члены ряда
оба расходятся. Это означает, что последовательности частичных сумм обоих рядов неограничены сверху. Будем выписывать по порядку неотрицательные члены ряда 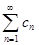 :
: 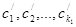
до тех пор пока не окажется, что
 ≥ 2.
≥ 2.
Затем начнём выписывать отрицательные члены ряда 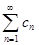 :
:
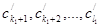
до тех пор, пока не окажется, что
 +
+ 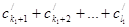 ≤ 1.
≤ 1.
После этого снова будем выписывать неотрицательные члены исходного ряда:
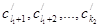
до тех пор, пока не окажется, что
 +
+ 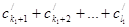 +
+ 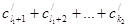 ≥ 2,
≥ 2,
а потом отрицательные члены и так далее.
Так как частичные суммы 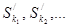 больше или равны 2, а все частичные суммы
больше или равны 2, а все частичные суммы 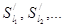 меньше или равны 1, то последовательность частичных сумм
меньше или равны 1, то последовательность частичных сумм 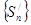 ряда
ряда 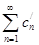 является расходящейся. Значит, ряд
является расходящейся. Значит, ряд 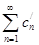 расходится.
расходится.
Второе утверждение теоремы доказывается аналогично.
Задачи.
6.1. Найти сумму ряда 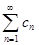 , где:
, где:
а) 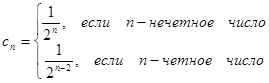 ;
;
б) 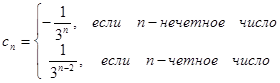 ;
;
в) 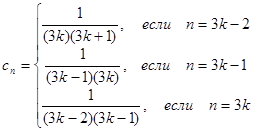 .
.
6.2. Члены сходящегоcя ряда 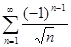 переставить так, чтобы он стал расходящимся.
переставить так, чтобы он стал расходящимся.
6.3. Исследовать на сходимость числовые ряды:
а) 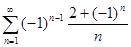 ; б)
; б) 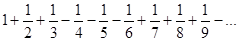 .
.
Дата добавления: 2016-07-09; просмотров: 2610;
