Основные утверждения о равномерно сходящихся функциональных последовательностях
Теорема 8.1. Последовательность {fn(x)} сходится на множестве V равномерно тогда и только тогда, когда для любого ε > 0 существует номер N = N(ε) (зависящий только от ε) такой, что при всех m, n ≥ N одновременно для всех 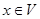 выполняется неравенство
выполняется неравенство
|fn(x) – fm(x)| < ε .
Доказательство необходимости. Если {fn(x)} 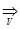 f(x), то для любогоε > 0 существует номер N = N(ε) такой, что при всех
f(x), то для любогоε > 0 существует номер N = N(ε) такой, что при всех 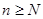 одновременно для всех x
одновременно для всех x 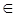 V выполняется неравенство |fn(x) – f(x)| <
V выполняется неравенство |fn(x) – f(x)| < 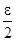 . Тогда при всех m, n ≥ N и всех
. Тогда при всех m, n ≥ N и всех 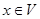 получим
получим
|fn(x) – fm(x)| = |fn(x) – f(x) + f(x) – fm(x) | ≤
≤ |fn(x) – f(x)| + |fm(x) – f(x)| < 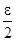 +
+ 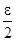 = ε.
= ε.
Доказательство достаточности. По условию, для любого ε > 0 существует номер N = N(ε) такой, что при всех m, n ≥ N одновременно для всех 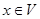 выполняется неравенство
выполняется неравенство
| fn(x) – fm(x)| < 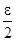 . (8.1)
. (8.1)
Это означает, что при каждом x  V числовая последовательность {fn(x)} является фундаментальной и, следовательно, она сходится. Положим
V числовая последовательность {fn(x)} является фундаментальной и, следовательно, она сходится. Положим 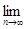 {fn(x)} = f(x), x
{fn(x)} = f(x), x  V. Из неравенства (8.1) следует, что при m, n ≥ N и любом x
V. Из неравенства (8.1) следует, что при m, n ≥ N и любом x  V выполняется неравенство
V выполняется неравенство
fm(x) − 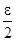 < fn(x) < fm(x) +
< fn(x) < fm(x) + 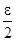 (8.2)
(8.2)
В неравенстве (8.2) зафиксируем n ≥ N и перейдем к пределу при
m → +∞. Получим
f (x) − 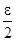 ≤ fn(x) ≤ f (x) +
≤ fn(x) ≤ f (x) + 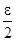 ,
,
где n ≥ N, x  V. Значит, |fn(x) – f (x)| <
V. Значит, |fn(x) – f (x)| < 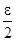 < ε, где n ≥ N, x
< ε, где n ≥ N, x  V.
V.
Таким образом, для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N одновременно для всех x  V выполняется неравенство |fn(x) – f (x)| < ε. Значит, {fn(x)}
V выполняется неравенство |fn(x) – f (x)| < ε. Значит, {fn(x)} 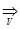 f(x).
f(x).
Пример. Рассмотрим последовательность {fn(x)}, где
 .
.
Покажем, что сходимость {fn(x)} на отрезке [0,1] не является равномерной. Если последовательность {fn(x)} сходится на отрезке [0,1] равномерно, то для  найдётся номер N такой, что при всех m, n ≥ N и всех
найдётся номер N такой, что при всех m, n ≥ N и всех 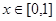 выполняется неравенство
выполняется неравенство
|fn(x) – fm(x)|  . (8.3)
. (8.3)
Если m = 2n, где n ≥ N , а x = 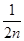 , то
, то 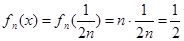 ,
,
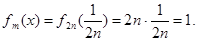 Тогда | fn(x) – fm(x)| = |
Тогда | fn(x) – fm(x)| = | 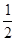 − 1| =
− 1| = 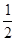 , что противоречит неравенству (8.3).
, что противоречит неравенству (8.3).
Теорема 8.2. Если {fn(x)} 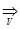 f(x), а все функции fn(x), n
f(x), а все функции fn(x), n  N, непрерывны на множестве V, то и функция f(x) непрерывна на множестве V.
N, непрерывны на множестве V, то и функция f(x) непрерывна на множестве V.
Доказательство. Пусть ε > 0 − произвольное положительное число. Так как {fn(x)} 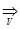 f(x), то существует номер N = N(ε) такой, что при всех n ≥ N и x
f(x), то существует номер N = N(ε) такой, что при всех n ≥ N и x  V выполняется неравенство |fn(x) – f(x)| <
V выполняется неравенство |fn(x) – f(x)| < 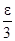 . Рассмотрим произвольную точку x0
. Рассмотрим произвольную точку x0  V. По условию, функция fN(x) непрерывна на множестве V, а, следовательно, и в точке x0. Это означает, что существует окрестность Sδ(x0) такая, что для любого
V. По условию, функция fN(x) непрерывна на множестве V, а, следовательно, и в точке x0. Это означает, что существует окрестность Sδ(x0) такая, что для любого 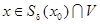 выполняется неравенство
выполняется неравенство
|fN(x) – fN(x0)| 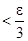 .
.
Тогда для любой точки 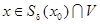 получим
получим
|f (x) – f (x0)| = |f (x) – fN(x) + fN(x) – fN(x0) + fN(x0) − f (x0)| ≤
≤ |f (x) – fN(x)| + | fN(x) − fN(x0)| + | fN(x0) − f (x0)| < 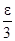 +
+ 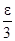 +
+ 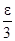 = ε.
= ε.
Таким образом для любого ε > 0 существует окрестность Sδ(x0) такая, что для всех x  Sδ(x0)∩V выполняется неравенство
Sδ(x0)∩V выполняется неравенство
|f (x) – f (x0)| < ε. Значит, функция f(x) непрерывна в точке x0. Теорема доказана.
Пример. 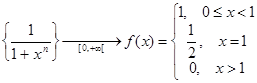 .
.
Все функции fn(x) = 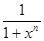 , n
, n  N, непрерывны на полуинтервале [0,+∞[, а функция f(x) имеет разрывы. Следовательно, сходимость на полуинтервале [0,+∞[ не является равномерной.
N, непрерывны на полуинтервале [0,+∞[, а функция f(x) имеет разрывы. Следовательно, сходимость на полуинтервале [0,+∞[ не является равномерной.
Теорема 8.3. Если {fn(x)}  f(x), а все функции fn(x), n
f(x), а все функции fn(x), n  N, непрерывны на отрезке [a,b], то
N, непрерывны на отрезке [a,b], то 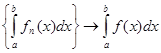 .
.
Доказательство. Пусть ε > 0 − произвольное положительное число. Из равномерной сходимости следует, что существует номер N = N(ε) такой, что при всех n ≥ N и x  [a,b] выполняется неравенство
[a,b] выполняется неравенство 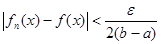 . Тогда, при
. Тогда, при
всех n ≥ N получим
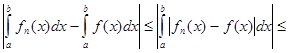
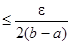 (b − a) =
(b − a) = 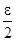 < ε.
< ε.
Таким образом, для любого ε > 0 существует номер N = N(ε) такой, что при всех n ≥ N выполняется неравенство 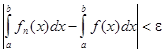 . Это означает, что числовая последовательность
. Это означает, что числовая последовательность 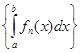 является сходящейся и имеет предел
является сходящейся и имеет предел 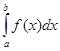 , то есть
, то есть 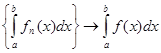 . Теорема доказана.
. Теорема доказана.
Пример. Функциональная последовательность 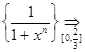 1. Функции fn(x) =
1. Функции fn(x) = 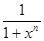 , n
, n  N, непрерывны на отрезке
N, непрерывны на отрезке 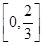 . Значит,
. Значит, 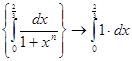 =
=  .
.
Теорема 8.4.Дана функциональная последовательность {fn(x)}, x  [a,b]. Предположим, что выполняются следующие условия:
[a,b]. Предположим, что выполняются следующие условия:
1) функции fn(x), n  N, непрерывно дифференцируемы на отрезке [a,b];
N, непрерывно дифференцируемы на отрезке [a,b];
2) {fn(x)} 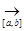 f(x);
f(x);
3) последовательность из производных {  (x)} сходится на отрезке [a,b] равномерно.
(x)} сходится на отрезке [a,b] равномерно.
Тогда функция f(x) непрерывно дифференцируема на отрезке [a,b], причём {  (x)}
(x)} 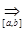
 (x).
(x).
Доказательство.Предположим, что {  (x)}
(x)} 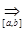 φ(x). Тогда по теореме 8.3
φ(x). Тогда по теореме 8.3 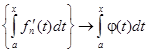 для каждого x
для каждого x  [a,b]. Так как
[a,b]. Так как 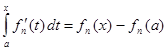 , а {fn(x)}
, а {fn(x)} 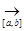 f(x) и {fn(a)} → f(a), то
f(x) и {fn(a)} → f(a), то 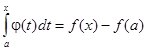 . По теореме о дифференцируемости интеграла по верхнему пределу
. По теореме о дифференцируемости интеграла по верхнему пределу  (x) = φ(x), где x
(x) = φ(x), где x  [a,b]. По теореме 8.2 функция φ(x) непрерывна на отрезке [a,b]. Значит, функция f(x) непрерывно дифференцируема на отрезке [a,b]. Теорема доказана.
[a,b]. По теореме 8.2 функция φ(x) непрерывна на отрезке [a,b]. Значит, функция f(x) непрерывно дифференцируема на отрезке [a,b]. Теорема доказана.
Пример. Дана функциональная последовательность {fn(x)}, сходящаяся на интервале ]−1,1[, где
fn(x) = 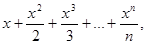 n
n  N.
N.
Пусть 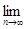 {fn(x)} = f(x), x
{fn(x)} = f(x), x  ]−1,1[. Найдем функцию f(x), используя теорему 8.4. Все функции fn(x), n
]−1,1[. Найдем функцию f(x), используя теорему 8.4. Все функции fn(x), n  N, непрерывно дифференцируемы на всей числовой прямой, причём
N, непрерывно дифференцируемы на всей числовой прямой, причём
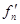 (x) = 1 + x + x2 + … + xn−1 =
(x) = 1 + x + x2 + … + xn−1 = 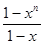 при x ≠ 1.
при x ≠ 1.
Нетрудно проверить, что { 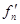 (x)}
(x)} 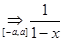 , где 0 < a < 1. Тогда по теореме 8.4
, где 0 < a < 1. Тогда по теореме 8.4
 (x)
(x)  , где
, где 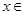 ]−1,1[.
]−1,1[.
Следовательно,
 .
.
Очевидно, что f(0) = 0. Тогда с = 0. Значит, f(x) = − ln(1 − x), где 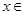 ]−1,1[ .
]−1,1[ .
Задачи.
8.1. Исследовать функциональную последовательность на равномерную сходимость:
а) 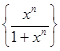 , x
, x  [
[ 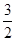 , + ∞[;
, + ∞[;
б) 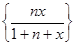 , x
, x  [0 , 1];
[0 , 1];
в)  , x
, x  ]− ∞ , + ∞[;
]− ∞ , + ∞[;
г) {arctg nx}, x  [1, +∞[;
[1, +∞[;
8.2. Найти:
а) 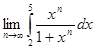 ; б)
; б) 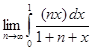 ;
;
в) 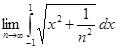 ; г)
; г) 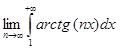 .
.
8.3. Найти 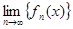 , если
, если
а) 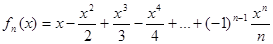 , x
, x  ]−1,1[ , n
]−1,1[ , n  N;
N;
б) 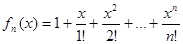 , x
, x  ]− ∞ , + ∞[, n
]− ∞ , + ∞[, n  N.
N.
Дата добавления: 2016-07-09; просмотров: 1118;
