Основные утверждения о сумме функциональных рядов
Если функциональный ряд 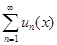 сходится на множестве W, то он имеет на этом множестве сумму S(x), то есть имеет место равенство
сходится на множестве W, то он имеет на этом множестве сумму S(x), то есть имеет место равенство 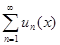 = S(x), где x
= S(x), где x  W .
W .
Теорема 10.1(о непрерывности суммы функционального ряда). Если функциональный ряд 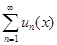 сходится к функции S(x) равномерно на множестве W, а все функции un(x) непрерывны на этом множестве, то функция S(x) непрерывна на множестве W.
сходится к функции S(x) равномерно на множестве W, а все функции un(x) непрерывны на этом множестве, то функция S(x) непрерывна на множестве W.
Доказательство. Положим Sn(x) = 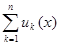 , x
, x  W , n
W , n  N. Все функции Sn(x) непрерывны на множестве W. По определению равномерной сходимости функционального ряда последовательность {Sn(x)}
N. Все функции Sn(x) непрерывны на множестве W. По определению равномерной сходимости функционального ряда последовательность {Sn(x)} 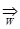 S (x) . Тогда по теореме 8.2 функция S(x) непрерывна на множестве W.
S (x) . Тогда по теореме 8.2 функция S(x) непрерывна на множестве W.
Пример.Дан функциональный ряд 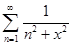 . Все члены этого ряда un(x) =
. Все члены этого ряда un(x) = 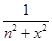 , n
, n  N, непрерывны на всей числовой прямой, а сам функциональный ряд
N, непрерывны на всей числовой прямой, а сам функциональный ряд 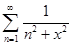 сходится на всей числовой прямой равномерно. Действительно,
сходится на всей числовой прямой равномерно. Действительно, 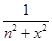 ≤
≤ 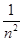 , где x
, где x  ]−∞,+∞[ , n
]−∞,+∞[ , n  N. Числовой ряд
N. Числовой ряд 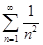 сходится. По признаку Вейерштрасса ряд
сходится. По признаку Вейерштрасса ряд 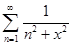 сходится равномерно на всей числовой прямой. Тогда по теореме 10.1. сумма функционального ряда
сходится равномерно на всей числовой прямой. Тогда по теореме 10.1. сумма функционального ряда 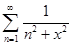 непрерывна на всей числовой прямой.
непрерывна на всей числовой прямой.
Теорема 10.2(о почленном интегрировании функционального ряда). Если функциональный ряд 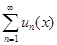 сходится к функции S(x) равномерно на отрезке [a,b], а все функции un(x) непрерывны на этом отрезке, то
сходится к функции S(x) равномерно на отрезке [a,b], а все функции un(x) непрерывны на этом отрезке, то
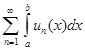 =
= 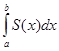 .
.
Доказательство. Положим Sn(x) = 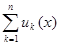 , x
, x  [a,b], n
[a,b], n  N. Все функции Sn(x) непрерывны на отрезке [a,b], причем {Sn(x)}
N. Все функции Sn(x) непрерывны на отрезке [a,b], причем {Sn(x)} 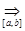 S(x). Тогда по теореме 8.3 (о почленном интегрировании функциональной последовательности)
S(x). Тогда по теореме 8.3 (о почленном интегрировании функциональной последовательности)
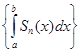 →
→ 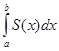 .
.
Это выражение можно записать в виде 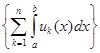 →
→ 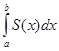 . Это и означает, что
. Это и означает, что
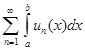 =
= 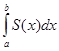 .
.
Пример.Функциональный ряд 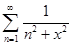 cходится на всей числовой прямой равномерно к некоторой функции S(x), а все члены этого ряда непрерывны. По теореме 10.2 для любого
cходится на всей числовой прямой равномерно к некоторой функции S(x), а все члены этого ряда непрерывны. По теореме 10.2 для любого
t  ]− ∞, + ∞[ имеет место равенство
]− ∞, + ∞[ имеет место равенство 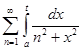 =
= 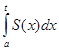 . Тогда
. Тогда 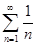 arctg
arctg 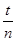 =
= 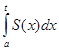 для любого t
для любого t  ]− ∞, + ∞[.
]− ∞, + ∞[.
Теорема 10.3(о почленном дифференцировании функционального ряда).
Дан функциональный ряд 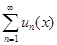 , где x
, где x  [a,b]. Пусть выполняются следующие условия:
[a,b]. Пусть выполняются следующие условия:
1) все члены ряда un(x), n  N, непрерывно дифференцируемы на отрезке [a,b];
N, непрерывно дифференцируемы на отрезке [a,b];
2) 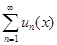 = S(x), где x
= S(x), где x  [a,b];
[a,b];
3) функциональный ряд из производных 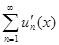 сходится на отрезке [a,b] равномерно.
сходится на отрезке [a,b] равномерно.
Тогда функция S(x) непрерывно дифференцируема на отрезке [a,b], причем
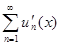 =
= 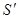 (x), где x
(x), где x  [a,b].
[a,b].
Доказательство. Положим Sn(x) = 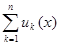 , x
, x  [a,b], n
[a,b], n  N. Тогда имеем:
N. Тогда имеем:
1) все функции Sn(x), n  N, непрерывно дифференцируемы на отрезке [a,b];
N, непрерывно дифференцируемы на отрезке [a,b];
2) функциональная последовательность частичных сумм ряда {Sn(x)}является сходящейся к функции S(x) на отрезке [a,b], т.е. {Sn(x)} 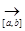 S (x);
S (x);
3) функциональная последовательность из производных 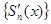 сходится на отрезке [a,b] равномерно.
сходится на отрезке [a,b] равномерно.
Тогда по теореме 8.4 функция S(x) непрерывно дифференцируема на отрезке [a,b], причем 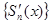
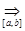
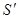 (x). Это означает, что
(x). Это означает, что 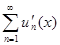 =
= 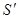 (x), где x
(x), где x 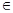 [a,b].
[a,b].
Пример.Рассмотрим функциональный ряд 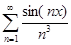 . Этот ряд сходится на всей числовой прямой. Значит,
. Этот ряд сходится на всей числовой прямой. Значит,
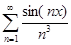 = f(x), где x
= f(x), где x  ]−∞,+∞[.
]−∞,+∞[.
Так как производная функции un(x) равна
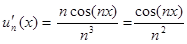 , x
, x  ]− ∞,+∞[ , то все члены ряда un(x) =
]− ∞,+∞[ , то все члены ряда un(x) = 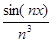 , n
, n  N, непрерывно дифференцируемы на всей числовой прямой. Функциональный ряд
N, непрерывно дифференцируемы на всей числовой прямой. Функциональный ряд 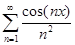 сходится на всей числовой прямой равномерно. По теореме 10.3 функция f(x) непрерывно дифференцируема на всей числовой прямой, причем
сходится на всей числовой прямой равномерно. По теореме 10.3 функция f(x) непрерывно дифференцируема на всей числовой прямой, причем
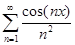 =
= 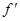 (x), где x
(x), где x  ]− ∞, + ∞[ .
]− ∞, + ∞[ .
Задачи.
10.1. Найти область определения функции f(x) и исследовать ее на непрерывность, если:
а) f(x) = 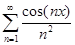 ; б) f(x) =
; б) f(x) = 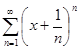 ;
;
в) f(x) = 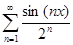 ; г) f(x) =
; г) f(x) = 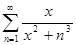 ;
;
д) f(x) = 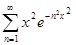 .
.
10.2. Доказать, что 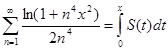 , где
, где
S(x) = 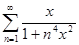 .
.
10.3. Доказать, что 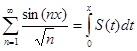 , где
, где
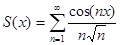 .
.
10.4. Найти сумму ряда 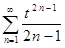 на множестве │t │< 1.
на множестве │t │< 1.
Указание. Использовать равенство 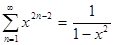 , x
, x  ]−1,1[.
]−1,1[.
10.5. Доказать, что функция f(x) дифференцируема, если:
а) f(x) = 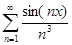 ; x
; x  ]− ∞, + ∞[ ;
]− ∞, + ∞[ ;
б) f(x) = 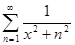 ; x
; x  ]− ∞, + ∞[ ;
]− ∞, + ∞[ ;
в) f(x) = 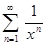 ; x
; x  ]1, + ∞[ ;
]1, + ∞[ ;
г) f(x) = 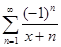 ; x
; x  [0, + ∞[ .
[0, + ∞[ .
10.6. Доказать, что функция f(x) =  непрерывна при x > 0 и вычислить
непрерывна при x > 0 и вычислить 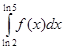 .
.
10.7. Доказать, что функция f(x) = 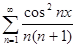 непрерывна на всей числовой прямой и вычислить
непрерывна на всей числовой прямой и вычислить 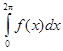 .
.
Дата добавления: 2016-07-09; просмотров: 1949;
