Доказательство. Докажем равенство 5). Известно, что
 =
= 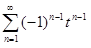 ; t
; t  ]−1, 1[ .
]−1, 1[ .
Это равенство можно проинтегрировать почленно на отрезке
[0, x], где x  ]−1, 1[ :
]−1, 1[ :
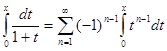 .
.
Тогда
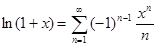 , x
, x  ]−1, 1[ .
]−1, 1[ .
Областью сходимости ряда 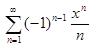 является полуинтервал
является полуинтервал
]−1, 1]. Следовательно,
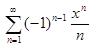 = S(x), x
= S(x), x  ]−1, 1] ,
]−1, 1] ,
причем функция S(x) непрерывна на полуинтервале ]−1, 1]. Так как S(x) = ln(1 + x), x  ]−1, 1[, то
]−1, 1[, то
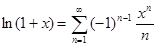 , x
, x  ]−1, 1] .
]−1, 1] .
Докажем равенство7). Степенной ряд
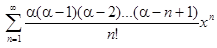
сходится на интервале ]−1, 1[, так как
 = =
= = 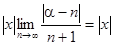 .
.
Тогда
1 + 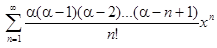 = S(x), x
= S(x), x  ]−1, 1[. (15.1)
]−1, 1[. (15.1)
Дифференцируя равенство (15.1) почленно, получим
α + 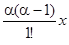 +
+  + … +
+ … + 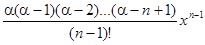 +
+
+ 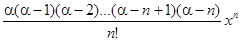 +… =
+… =  (x), x
(x), x  ]−1,1[. (15.2)
]−1,1[. (15.2)
Тогда αx +  +
+ 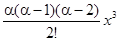 +
+
… +  +
+
+ 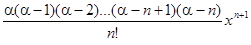 + … = x
+ … = x  (x), (15.3)
(x), (15.3)
где x  ]−1, 1[. Сложив равенства (15.2) и (15.3), получим
]−1, 1[. Сложив равенства (15.2) и (15.3), получим
α + 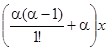 +
+ 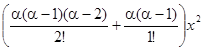 + … + +
+ … + + 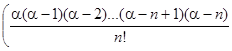 + +
+ + 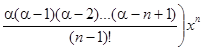 + … =
+ … =  (x)(1+x).
(x)(1+x).
Тогда
α + 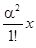 +
+ 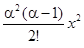 + … +
+ … +  +…
+…
… =  (x)(1+x).
(x)(1+x).
Следовательно,
α · S(x) =  (x)(1 + x), x
(x)(1 + x), x  ]−1, 1[.
]−1, 1[.
Если f (x) = S (x)(1+x)−α, то
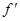 (x) =
(x) =  (x)(1+x)−α − α S (x)(1+x)−α−1 =
(x)(1+x)−α − α S (x)(1+x)−α−1 =
=  (x)(1+x)−α −
(x)(1+x)−α −  (x)(1+x)(1+x)−α−1 = 0, x
(x)(1+x)(1+x)−α−1 = 0, x  ]−1, 1[.
]−1, 1[.
Тогда f (x) = c, x  ]−1, 1[. Значит, S(x) = c(1 + x)α, x
]−1, 1[. Значит, S(x) = c(1 + x)α, x  ]−1, 1[. Из равенства (15.1) следует, что S(0) = 1. Тогда c = 1. Следовательно
]−1, 1[. Из равенства (15.1) следует, что S(0) = 1. Тогда c = 1. Следовательно
S(x) = (1 + x)α, x  ]−1, 1[.
]−1, 1[.
Замечание.Соотношения 1) – 7), приведенные в теореме 15.1, широко используются для разложения различных функций в степенные ряды.
Примеры.1. Чтобы разложить функцию f (x) = 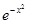 в ряд по степеням x, рассмотрим равенство
в ряд по степеням x, рассмотрим равенство
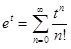 , t
, t  ]−∞, +∞[ .
]−∞, +∞[ .
Положим t = − x2. Тогда
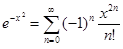 , x
, x  ]−∞, +∞[ .
]−∞, +∞[ .
2.Рассмотрим функцию f (x) = 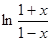 . Заметим, что
. Заметим, что
 =
= 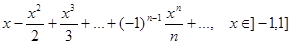 ;
;
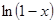 =
= 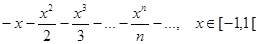 .
.
Тогда при x  ]−1, 1[ получим:
]−1, 1[ получим:
f (x) = 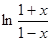 =
=  −
− 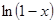 = =
= = 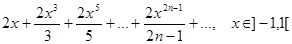 .
.
3.Рассмотрим разложение
(1+ t)α = 1 + 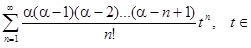 ]−1,1[.
]−1,1[.
Пусть α = 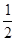 , тогда
, тогда
 = 1 +
= 1 + 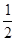 t +
t + 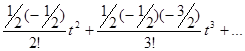
+ 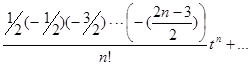
Таким образом,
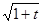 = 1+
= 1+ 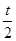 +
+ 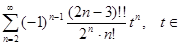 ]−1,1[ .
]−1,1[ .
Следовательно,
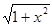 = 1 +
= 1 +  +
+ 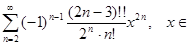 ]−1,1[ .
]−1,1[ .
4. Разложим функцию f (x) = 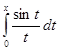 по степеням x. Рассмотрим равенство
по степеням x. Рассмотрим равенство
sin t = 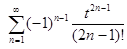 , t
, t  ]−∞, +∞[ .
]−∞, +∞[ .
Если t ≠ 0, то
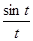 =
=  .
.
Следовательно, 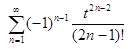 = φ(t), t
= φ(t), t  ]−∞, +∞[ ,
]−∞, +∞[ ,
где
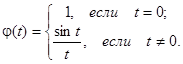
Тогда
f (x) = 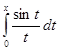 =
= 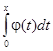 =
=
= 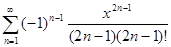 , x
, x  ]−∞, +∞[ .
]−∞, +∞[ .
Задачи.
15.1. Разложить функцию f (x) в ряд по степеням x, если:
а) f (x) = 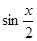 ; б) f (x) =
; б) f (x) =  ;
;
в) f (x) = 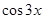 ; г) f (x) =
; г) f (x) = 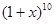 ;
;
д) f (x) = 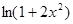 ; е) f (x) =
; е) f (x) = 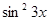 ;
;
ж) f (x) = arctg  ; з) f (x) =
; з) f (x) = 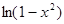 .
.
15.2. Разложить функцию f (x) в ряд по степеням x, если:
а) f (x) =  ; б) f (x) =
; б) f (x) =  ;
;
в) f (x) =  ; г) f (x) =
; г) f (x) = 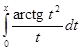 .
.
15.3. Разложить функцию f (x) в ряд по степеням (x − x0), если:
а) f (x) = lnx, x0 = 1; б) f (x) = 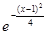 , x0 = 1;
, x0 = 1;
в) f (x) = 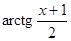 , x0 = −1; г) f (x) =
, x0 = −1; г) f (x) = 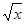 , x0 = 4;
, x0 = 4;
д) f (x) =  , x0 =
, x0 = 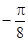 ; е) f (x) =
; е) f (x) = 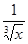 , x0 = 1.
, x0 = 1.
Дата добавления: 2016-07-09; просмотров: 802;
