Равномерная сходимость степенных рядов
Лемма 1. Степенной ряд 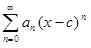 сходится равномерно и абсолютно на любом отрезке внутри интервала сходимости ]c−R, c+R[.
сходится равномерно и абсолютно на любом отрезке внутри интервала сходимости ]c−R, c+R[.
Доказательство. Предположим, что [a, b] 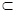 ]c − R , c + R [ , где R > 0. Тогда │a − c │< R и │ b − c │< R . Положим
]c − R , c + R [ , где R > 0. Тогда │a − c │< R и │ b − c │< R . Положим
d = max{│ a − c │, │ b − c │}. Если x  [a, b], то │x − c│ ≤ d . Тогда │an│·│x − c│n ≤ │an│·d n, n
[a, b], то │x − c│ ≤ d . Тогда │an│·│x − c│n ≤ │an│·d n, n  N. Степенной ряд
N. Степенной ряд 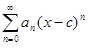 сходится абсолютно при x = c + d, поскольку x − c = d < R. Это означает, что сходится числовой ряд
сходится абсолютно при x = c + d, поскольку x − c = d < R. Это означает, что сходится числовой ряд 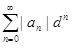 . Тогда степенной ряд
. Тогда степенной ряд 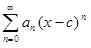 сходится равномерно и абсолютно на отрезке [a,b] по признаку Вейерштрасса.
сходится равномерно и абсолютно на отрезке [a,b] по признаку Вейерштрасса.
Лемма 2. Если степенной ряд 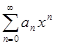 сходится при x = R, то он сходится равномерно на отрезке [0, R].
сходится при x = R, то он сходится равномерно на отрезке [0, R].
Доказательство. По условию, числовой ряд  сходится. Значит, последовательность частичных сумм этого ряда является фундаментальной. Тогда для любого ε > 0 существует номер N = N(ε) такой, что при всех m, n ≥ N выполняется неравенство |Sn – Sm| < ε. Если n > m ≥ N, то
сходится. Значит, последовательность частичных сумм этого ряда является фундаментальной. Тогда для любого ε > 0 существует номер N = N(ε) такой, что при всех m, n ≥ N выполняется неравенство |Sn – Sm| < ε. Если n > m ≥ N, то
|anRn + an-1Rn-1 + … + am+2Rm+2 + am+1Rm+1| < ε.
Положим
Bm+1 = am+1Rm+1,
Bm+2 = am+1Rm+1 + am+2Rm+2 ,
…
Bn = am+1Rm+1 + am+2Rm+2 + …+ an-1Rn-1 + anRn .
Тогда
|Bm+1| < ε, |Bm+2| < ε, … , |Bn| < ε,
причём:
am+1Rm+1 = Bm+1,
am+2Rm+2 = Bm+2 − Bm+1 ,
…
anRn = Bn − Bn-1.
Рассмотрим последовательность частичных сумм {Sn(x)} степенного ряда 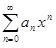 . Если x
. Если x  [0, R], а n > m ≥ N, то
[0, R], а n > m ≥ N, то
| Sn (x) − Sm (x)| = | an ·xn + an−1·xn−1 + …+ am+1·xm+1 | =
= | an · R n 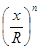 + an−1· R n−1
+ an−1· R n−1 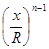 +… + am+1· R m+1
+… + am+1· R m+1 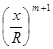 | =
| =
= |(Bn − Bn−1) 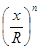 + (Bn−1 − Bn−2)
+ (Bn−1 − Bn−2) 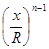 +…+ Bm+1
+…+ Bm+1 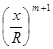 | =
| =
= |Bn 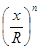 + Bn−1(
+ Bn−1(  −
− 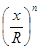 ) + …+ Bm+1(
) + …+ Bm+1( 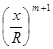 −
− 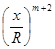 )| ≤
)| ≤
≤| Bn|· 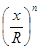 + |Bn−1|(
+ |Bn−1|( 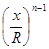 −
− 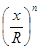 ) +.. + |Bm+1|(
) +.. + |Bm+1|( 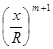 −
− 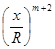 ) <
) <
< ε ( 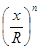 +
+ 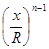 −
− 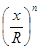 +… +
+… + 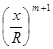 −
− 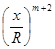 ) = ε
) = ε 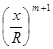 ≤ ε.
≤ ε.
Аналогично можно показать, что при m > n ≥ N и всех x  [0, R] выполняется неравенство
[0, R] выполняется неравенство
| Sm (x) − Sn (x) | < ε.
Таким образом, для любого ε > 0 существует номер N = N(ε) такой, что при всех m, n ≥ N одновременно для всех x  [0, R] выполняется неравенство
[0, R] выполняется неравенство
| Sn (x) − Sm (x) | < ε.
По утверждению 2 (раздел 9) степенной ряд  сходится равномерно на отрезке [0, R].
сходится равномерно на отрезке [0, R].
Следствие. Если степенной ряд 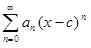 сходится при x = c + R, где R > 0, то он сходится равномерно на отрезке
сходится при x = c + R, где R > 0, то он сходится равномерно на отрезке
[c, c + R]. Если степенной ряд 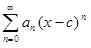 сходится при x = c −R, где R > 0, то он сходится равномерно на отрезке [c − R, c].
сходится при x = c −R, где R > 0, то он сходится равномерно на отрезке [c − R, c].
Доказательство.Предположим, что степенной ряд 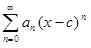 сходится при x = c + R. Тогда степенной ряд
сходится при x = c + R. Тогда степенной ряд 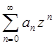 , где z = x − c, будет сходиться при z = R. По лемме 2 этот ряд сходится равномерно на отрезке [0,R]. Тогда исходный ряд
, где z = x − c, будет сходиться при z = R. По лемме 2 этот ряд сходится равномерно на отрезке [0,R]. Тогда исходный ряд 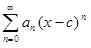 сходится равномерно на отрезке [c, c + R].
сходится равномерно на отрезке [c, c + R].
Если же степенной ряд 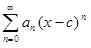 сходится при x = c − R, то степенной ряд
сходится при x = c − R, то степенной ряд 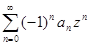 , где z = x − c, сходится при z = R. По лемме 2 степенной ряд
, где z = x − c, сходится при z = R. По лемме 2 степенной ряд 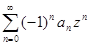 сходится равномерно на отрезке [0,R]. Тогда исходный степенной ряд
сходится равномерно на отрезке [0,R]. Тогда исходный степенной ряд 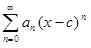 сходится равномерно на отрезке [c − R, c].
сходится равномерно на отрезке [c − R, c].
Теорема 12.1.Степенной ряд 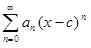 сходится равномерно на любом отрезке в его области сходимости.
сходится равномерно на любом отрезке в его области сходимости.
Доказательство. Если область сходимости степенного ряда Ω совпадает с его интервалом сходимости, то утверждение теоремы сразу следует из леммы 1.
Предположим, что Ω − полуинтервал, т.е. Ω = ] c − R, c + R], где R > 0, а отрезок [a, c + R] 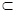 Ω. Можно считать, что a < c. Тогда по леммам 1 и 2 данный степенной ряд сходится равномерно на отрезках [a, c] и [c, c+R]. Следовательно, степенной ряд
Ω. Можно считать, что a < c. Тогда по леммам 1 и 2 данный степенной ряд сходится равномерно на отрезках [a, c] и [c, c+R]. Следовательно, степенной ряд 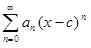 сходится равномерно на объединении этих отрезков [a, c]
сходится равномерно на объединении этих отрезков [a, c]  [c, c +R]=[a, c + R]. Остальные возможные случаи, когда Ω = [c − R, c + R[ или
[c, c +R]=[a, c + R]. Остальные возможные случаи, когда Ω = [c − R, c + R[ или
Ω = [c − R, c + R], рассматриваются аналогично.
Пример.Дан степенной ряд  . Тогда
. Тогда
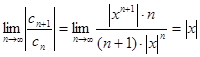 .
.
Следовательно, степенной ряд сходится абсолютно при |x| < 1 и расходится при |x| > 1. В точке x = 1 имеем числовой ряд  , который сходится по теореме Лейбница. При x = − 1 получаем гармонический ряд
, который сходится по теореме Лейбница. При x = − 1 получаем гармонический ряд 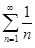 , который расходится. Значит, область сходимости данного степенного ряда Ω = ]−1, 1]. По теореме 12.1, степенной ряд
, который расходится. Значит, область сходимости данного степенного ряда Ω = ]−1, 1]. По теореме 12.1, степенной ряд  сходится равномерно на любом отрезке [a, 1]
сходится равномерно на любом отрезке [a, 1]  ]−1, 1].
]−1, 1].
Задачи.
12.1. Исследовать степенной ряд на равномерную сходимость:
а) 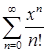 ; б)
; б) 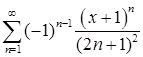 ;
;
в) 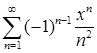 ; г)
; г) 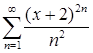 ;
;
д) 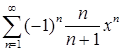 ; е)
; е) 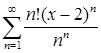 .
.
Дата добавления: 2016-07-09; просмотров: 3678;
