Аналитическое выравнивание временных рядов. Оценка параметров уравнения тренда.

Как уже отмечено выше, одной из важнейших задач исследования экономического временного ряда является выявление основной тенденции изучаемого процесса, выраженной неслучайной составляющей ¦ (t) (тренда либо тренда с циклической или (и) сезонной компонентой).

Для решения этой задачи вначале необходимо выбрать вид функции:

линейная - ¦ (t) = b₀ + b₁t,

полиноминальная - ¦ (t) = b₀ + b₁t + b₂t² + ….+ b_ntⁿ;

экспоненциальная - ¦ (t) = ;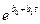

логистическая - ¦ (t)= ;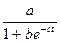

Гомперца - log ¦ (t) = a- br^t , где 0 < r < 1.

Это весьма ответственный этап исследования. При выборе соответствующей функции ¦(t) используют содержательный анализ ( который может установить характер динамики процесса), визуальные наблюдения( на основе графического изображения временного ряда). При выборе полиномиальной функции может быть применен метод последовательных разностей (состоящий в вычислении разностей первого порядка D_t = y_t + y_t-1 . второго порядка D_t⁽²⁾ = D_t + D_t – ₁ и т.д.), и порядок разностей, при котором они будут примерно одинаковыми, принимается степень полинома.

Из двух функций предпочтение обычно отдается той, при которой меньше сумма квадратов отклонений фактических данных от расчетных на основе этих функций. Но этот принцип нельзя доводить до абсурда: так, для любого ряда из n точек можно подобрать полином (n-1)-й степени, проходящий через все точки, и соответственно с минимальной – нулевой – суммой квадратов отклонений, но этом случае, очевидно, не следует говорить о выделении основной тенденции, учитывая случайный характера этих точек. Поэтому при прочих равных условиях предпочтение следует отдавать более простым функциям.

Для выявления основной тенденции чаще всего используется метод наименьших квадратов, рассмотренный в гл.3. Значения временного ряда y_t рассматриваются как зависимая переменная, а время t – как объясняющая:

y_t = ¦(t) + e_t , (6.7)

где e_t – возмущения, удовлетворяющие основным предпосылкам регрессионного анализа, приведенным в §3.4, т.е. представляющие независимые и одинаково распределенные случайные величины, распределение которых предполагаем нормальным.

Напомните, что согласно методу наименьших квадратов параметры прямой ŷ_t = ¦ (t) = b₀ + b₁t находимся из системы нормальных уравнений (3.5), в которой в качестве x_i берем t:

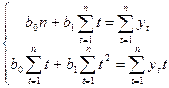(6.8)

Учитывая, что значения переменной t = 1,2,…,n образуют натуральный ряд чисел от 1 до n, суммы 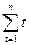, 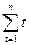² можно выразить через число членов ряда n по известным в математике формулам:

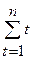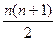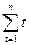= ; ² = 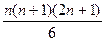. (6.9)

►Пример 6.2.

По данным табл. 6.1. найти уравнение неслучайной составляющей (тренда) для y_t , полагая тренд линейным.

Решение. По формуле (6.9)

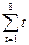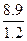= = 36 ; 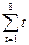² = 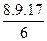= 204.

Далее

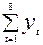= 213 + 171 +….+361 = 2375;

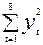= 213² + 171² +….+ 361² = 739827;

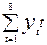= 213.1 + 171.2 +….+ 361.8 = 11766.

Система нормальных уравнений (6.8) имеет вид:

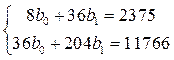
Откуда b₀ = 181,32; b₁ = 25,679 и уравнение тренда ŷ_t = 181,32 + 25,679t (рис 6.1), т.е. спрос ежегодно увеличивается в среднем на 25,7 ед.

При решении задачи можно было не выписывать систему нормальных уравнений, а представить уравнение регрессии в виде (3.12), т.е.

ŷ - 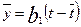, где

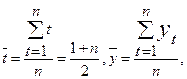
а коэффициент регрессии b₁ найти по формуле (3.13):

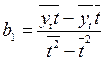
где

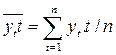
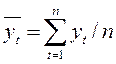
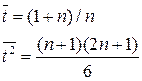
Проверим значимость полученного уравнения тренда по F – критерию на 5%-ном уровне значимости. Вычислим с помощью формулы (3.40) суммы квадратов:

а) обусловленную регрессией –

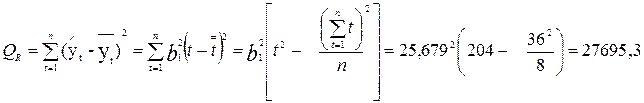б) общую –

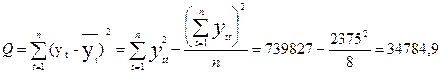
в) остаточную –

Q_e = Q – Q_R = 3478, 9 – 27695, 3 = 7053, 6.

Найдем по формуле (3.44) значение статистики:

F =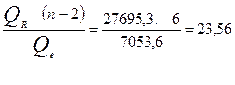

Так как F > F _0,05;1;6 ( см. табл. IV приложений), то уравнение тренда значимо.►

При применении метода наименьших квадратов для оценки парпметров экспоненциальной, логистической функций или функции Гомперца возникают сложности с решением получаемой системы нормальных уравнений, поэтому предварительно, до получения соответствующей системы, прибегают к некоторым преобразованиям этих функций ( например, логарифмированию и др.) (см. § 5.5).

Другим методом выравнивания (сглаживаний) временного ряда, т.е. выделения неслучайной составляющей, является метод скользящих средних.Он основан на переходе от наличных значений членов ряда к их средним значениям на интервале времени, длина которого определена заранее. При этом сам выбранный интервал времени «скользит» вдоль ряда.

Получаемый таким образом ряд скользящих средних ведет себя более гладко, чем исходный ряд, из-за усреднения отклонений ряда. Действительно , если индивидуальный разброс значений члена временного ряда (y_{1 +} y₂+…. +y_m )/m около своего среднего (сглаженного) значения а будет характеризоваться существенно меньшей величиной дисперсии, равной s²/m.

Для усреднения могут быть использованы средняя арифметическая ( простая и с некоторыми весами), медиана и др.

►Пример 6.3. Провести сглаживание временного ряда y_t по данным табл.6.1 методом скользящих средних, используя простую среднюю арифметическую с интервалом сглаживания m = 3 года.

Решение. Скользящие средние находим по формуле:

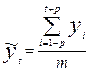(6.10)

Когда m=(2p-1) – нечетное число; при m=3 p=1.

Например, при t =2 по формуле (6.10):

;

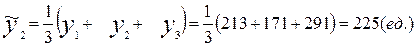При t=3

;

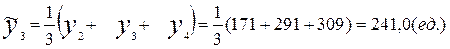В результате получим сглаженный ряд:

t
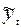
	-	225,0	241,0	305,7	329,3	336,3	358,0	-

На рис.6.1 этот ряд изображен графически в виде пунктирной линии.